Definición de fracción
Una fracción es un número que representa una o varias partes de uno o más enteros divididos en partes iguales. Se representa mediante dos números separados por una línea horizontal de la siguiente manera: \[\frac{a}{b}\] donde \(a\) y \(b\) son números enteros y \(b\) es diferente de cero.
Términos de una fracción
Los términos de una fracción son el numerador \(a\) y el denominador \(b\). El denominador indica en cuántas partes iguales se ha dividido el entero, mientras que el numerador indica cuántas partes se están tomando de esta división.

Ejemplos de fracciones
Ejemplo 1. En la fracción \(2/3\), el denominador, representado por el número 3, indica que un entero ha sido dividido en tres partes iguales. El numerador, que es el número 2, señala que se están tomando dos de las tres divisiones disponibles.
Ejemplo 2. En la fracción \(5/8\), el denominador, representado por el número 8, indica que un entero se ha dividido en 8 partes iguales. El numerador, que es el número 5, indica que se están tomando 5 de las 8 divisiones.
Ejemplo 3. Considera la fracción \(8/9\). En este caso, el denominador, representado por el número 9, indica que un entero ha sido dividido en 9 partes iguales. El numerador, que es el número 8, señala que se están tomando 8 de las 9 partes en las que se dividió el entero.

¿Qué es un entero en las fracciones?
Un entero, también conocido como unidad, representa todo aquello que está completo, es decir, algo que no le sobra ni le falta nada. En el contexto de las fracciones, un entero puede ser un objeto, una cosa o un número.
¿Cómo se lee una fracción?
Para leer una fracción, primero se enuncia el numerador y luego el denominador.
Cuando el numerador es 1, se lee como "un"; en caso de ser diferente de 1, se lee de acuerdo con su valor numérico. Por ejemplo, si el numerador es 2, se lee como "dos"; si es 11, se dice "once"; si es 17, se pronuncia "diecisiete"; y así sucesivamente.
En cuanto al denominador, cuando es 2, se lee como "medio"; si es 3, se dice "tercio"; si es 4, se pronuncia "cuarto"; si es 5, se lee "quinto"; si es 6, se dice "sexto"; si es 7, se pronuncia "séptimo"; si es 8, se lee "octavo"; si es 9, se dice "noveno"; y si es 10, se pronuncia "décimo". Para denominadores mayores a 10, se agrega la terminación "avo" a la pronunciación del número. Por ejemplo, si es 11, se lee como "onceavo"; si es 12, se dice "doceavo"; si es 16, se pronuncia "dieciseisavo"; y así sucesivamente.
Ejemplos de cómo leer una fracción
La fracción \(1/2\) se lee: un medio. La fracción \(1/10\) se lee: un décimo, la fracción \(2/3\) se lee: dos tercios, la fracción \(1/12\) se lee: un doceavo, la fracción \(4/11\) se lee: cuatro onceavos, la fracción \(23/31\) se lee: veintitrés treintaiunavos.
Tipos de fracciones
Las fracciones se dividen principalmente en fracciones comunes y fracciones decimales. A su vez, estas pueden clasificarse como fracciones propias, fracciones impropias o fracciones iguales a la unidad. A continuación, veremos la definición de cada tipo, así como una clave para que aprendas a identificarlas.
Fracciones comunes
Una fracción común es aquella en la que el denominador no es igual a la unidad seguida de ceros, es decir, aquella en la que el denominador no es 10, 100, 1000, etc. Por ejemplo, la fracción \(1/2\) es una fracción común, ya que el denominador es 2, es decir, es diferente a la unidad seguida de ceros. La facción \(10/3\) es una fracción común, debido a que el denominador es 3, y 3 es diferente a la unidad seguida de ceros.
Fracciones decimales
Una fracción decimal es aquella en la que el denominador es igual a la unidad seguida de ceros, es decir, aquella en la que el denominador es igual a 10, 100, 1000, etc. Por ejemplo, la fracción \(1/10\) es una fracción decimal, ya que el denominador es 10, es decir, la unidad seguida de un cero. La fracción \(11/100\) es una fracción decimal, ya que el denominador es igual a la unidad seguida de dos ceros.
Fracciones propias
Las fracciones propias son aquellas en las que el valor del numerador es menor que el valor del denominador. Una característica fundamental de las fracciones propias es que representan siempre una cantidad menor que la unidad completa. Por ejemplo, la fracción \(3/5\) es una fracción propia, ya que el numerador es menor que el denominador, pues 3 es menor que 5. La fracción \(1/2\) es una fracción propia, esto debido a que el numerador es menor que el denominador, ya que 1 es menor que 2. La fracción \(8/10\) es una fracción propia, pues el numerador es menor que el denominador.

Toda fracción propia es menor que la unidad. Para hacer evidente esto, tomemos la fracción \(3/5\), el denominador es el número 5 e indica que la unidad ha sido dividida en 5 partes iguales, el numerador es el número 3 e indica que se están tomando únicamente 3 de las 5 partes disponibles, así que faltaría tomar 2 partes para completar las 5, es decir, completar la unidad.
Fracciones impropias
Las fracciones impropias son aquellas en las que el valor del numerador es mayor que el valor del denominador. Estas fracciones representan siempre una cantidad mayor que la unidad completa. Por ejemplo, la fracción \(5/2\) es una fracción impropia, ya que el numerador es mayor que el denominador pues 5 es mayor que 2. La fracción \(18/5\) es una fracción impropia, esto debido a que el numerador es mayor que el denominador, es decir, 18 es mayor a 5.
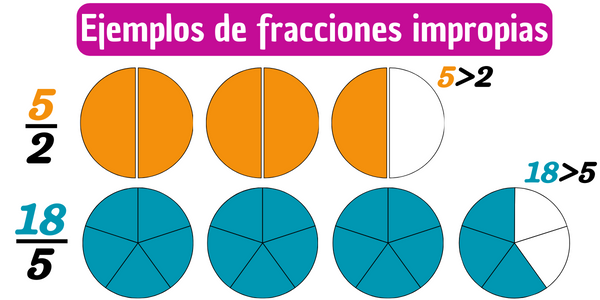
Toda fracción impropia es mayor que la unidad. Para hacer evidente esto, tomemos la fracción \(18/5\), el denominador es el número 5 e indica que la unidad ha sido dividida en 5 partes iguales, el numerador es el número 18 e indica que se están tomando 18 partes, pero este excede el número de partes disponibles, por lo que hace falta dividir más de una unidad en 5 partes iguales para completar las 18 que se requieren.
Fracciones iguales a la unidad
Una fracción igual a la unidad es aquella en la que el numerador es igual al denominador. Por ejemplo, la fracción \(2/2\) es una fracción igual a la unidad, ya que el numerador es igual al denominador. La fracción \(18/18\) es también una fracción igual a la unidad, esto porque el numerador es igual al denominador y la fracción \(11/11\) es también una fracción igual a la unidad pues el numerador es igual al denominador.
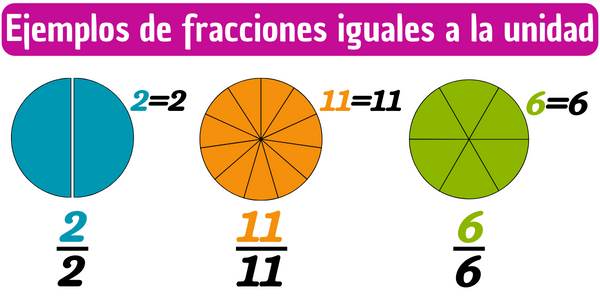
Este tipo de fracciones son iguales a la unidad debido a que al ser el numerador y el denominador iguales, nos indica que se están tomando todas las partes en las que fue dividida la unidad. Así en la fracción \(18/18\), el denominador es el número 18 e indica que la unidad ha sido dividida en 18 partes iguales, el numerador es el número 18 e indica que se están tomando 18 partes de las 18 disponibles, es decir, se está tomando toda la unidad completa.
Fracciones mixtas
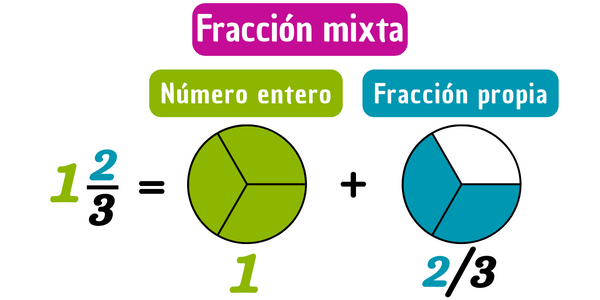
Las fracciones mixtas, también conocidas como números mixtos, son una combinación de una parte entera y una fracción propia. Una fracción mixta se representa como: \[a\frac{b}{c}\] donde \(a\) es la parte entera, \(b\) es el numerador y \(c\) es el denominador de la fracción propia. Por ejemplo, \(1\frac{2}{3}\) es una fracción mixta (número mixto), donde 1 es la parte entera y \(2/3\) es la fracción propia. La característica principal de las fracciones mixtas es que se pueden convertir en fracciones impropias y viceversa, ya que ambas se utilizan para representar cantidades que son mayores que la unidad.
Fracciones equivalentes
Las fracciones equivalentes son aquellas que representan la misma cantidad, pero que están escritas con diferentes numeradores y denominadores.
Se obtienen fracciones equivalentes al multiplicar o dividir tanto el numerador como el denominador de una fracción por el mismo número. Matemáticamente, si \(a/b\) es una fracción, entonces: \[\frac{ka}{kb}\] es una fracción equivalente, donde \(k\) es un número entero distinto de cero. Por ejemplo, las fracciones \(1/2\), \(2/4\) y \(3/6\) son equivalentes porque todas representan la mitad de un entero, es decir, representan siempre la misma cantidad, aunque estén escritas de manera diferente.

Álgebra de fracciones
El álgebra de fracciones implica realizar operaciones algebraicas, tales como la suma, la resta, la multiplicación, la división y la simplificación con fracciones. A continuación, veremos cómo se realiza cada una de estas operaciones.
Suma y resta de fracciones
Para sumar o restar fracciones, es necesario que estas tengan el mismo denominador. Si tienen denominadores diferentes, primero se deben encontrar fracciones equivalentes con el mismo denominador (común denominador). Una vez que las fracciones tengan el mismo denominador, para sumarlas o restarlas se suman o restan los numeradores y se conserva el mismo denominador. Por ejemplo, para determinar el valor de la siguiente suma de fracciones: \[\frac{5}{6}+\frac{3}{8}\] La fracción \(5/6\) y \(3/8\) reducidas a su mínimo común denominador son \(20/24\) y \(9/24\) respectivamente, por lo tanto: \[\begin{aligned}\frac{5}{6}+\frac{3}{8}&=\frac{20}{24}+\frac{9}{24}\\&=\frac{20+9}{24}\\&=\frac{29}{24}\end{aligned}\]
Multiplicación de fracciones
Para multiplicar dos o más fracciones, simplemente se multiplican los numeradores entre sí para obtener el nuevo numerador y los denominadores entre sí para obtener el nuevo denominador. Por ejemplo, para realizar la siguiente multiplicación de fracciones: \[\frac{3}{5}\cdot\frac{9}{2}\] La solución es: \[\begin{aligned}\frac{3}{5}\cdot\frac{9}{2}&=\frac{3\cdot 9}{5\cdot 2}\\&=\frac{27}{10}\end{aligned}\]
División de fracciones
Para dividir una fracción entre otra, se multiplica la primera fracción por el inverso (recíproco) de la segunda fracción. Es decir, se multiplica el numerador de la primera fracción por el denominador de la segunda y el numerador de la segunda fracción por el denominador de la primera. El resultado de esta multiplicación es la división de las fracciones. Por ejemplo, para hallar el valor de la siguiente división de fracciones: \[\frac{2}{3}\div\frac{1}{2}\] La solución es: \[\begin{aligned}\frac{2}{3}\div\frac{1}{2}&=\frac{2}{3}\cdot\frac{2}{1}\\&=\frac{2\cdot 2}{3\cdot 1}\\&=\frac{4}{3}\end{aligned}\]
Simplificación de fracciones
Para simplificar una fracción a su mínima expresión, se divide tanto el numerador como el denominador por su máximo común divisor. Por ejemplo, para simplificar a su mínima expresión la siguiente fracción: \[\frac{96}{128}\] Como el máximo común divisor (MCD) de 96 y 128 es 32, dividimos tanto el numerador como el denominador por este valor para obtener la fracción equivalente reducida a su mínima expresión: \[\begin{aligned}\frac{96}{128}&=\frac{96\div 32}{128\div32}\\&=\frac{3}{4}\end{aligned}\] Por lo tanto, la fracción reducida a su mínima expresión de \(98/128\) es \(3/4\).
¿Una fracción puede interpretarse como una división?
Si. Una fracción es el resultado de una división, es decir, una fracción es el cociente de una división, en la que el numerador representa el dividendo y el denominador representa al divisor.

Por ejemplo, la fracción 2/3 es el cociente de la división en la que el numerador 2 es el dividendo y el denominador 3 es el divisor. La fracción 5/7 es el cociente de la división en la que el numerador 5 es el dividendo y el denominador 7 es el divisor.
Preguntas frecuentes
¿Qué es una fracción? Una fracción es la expresión matemática que representa una o varias partes iguales de la unidad principal.
¿Cuál es la diferencia entre numerador y denominador? El numerador es el número situado arriba de la línea en una fracción y representa la cantidad de partes que se toman del entero. El denominador, ubicado debajo de la línea, representa el número de partes en que se divide el entero.
¿Qué es una fracción propia? Una fracción propia es aquella en la que el numerador es menor que el denominador. Una fracción propia representa una cantidad menor que la unidad.
¿Qué es una fracción impropia? Una fracción impropia es aquella en la que el numerador es mayor que el denominador. Una fracción impropia representa una cantidad mayor que la unidad y se puede expresar como un número entero y una fracción propia.
¿Qué son las fracciones equivalentes? La fracciones equivalentes son aquellas que representan la misma cantidad, pero están escritas de manera diferente. Para obtener fracciones equivalentes, se multiplican o dividen tanto el numerador como el denominador por un mismo número.
¿Cómo se simplifican las fracciones? Para simplificar una fracción, se divide tanto el numerador como el denominador por su máximo común divisor (MCD), obteniendo así una fracción equivalente en su forma más reducida.
¿Qué es el mínimo común múltiplo (MCM)? El mínimo común múltiplo (MCM) es el número más pequeño que es múltiplo de dos o más números. Se utiliza para encontrar un denominador común cuando se suman o restan fracciones con diferentes denominadores.
¿Qué es una fracción mixta? Una fracción mixta es aquella que combina un número entero con una fracción propia. Una fracción mixta es útil para expresar cantidades enteras y fraccionarias al mismo tiempo.
¿Cuál es la relación entre las fracciones y las razones? Las fracciones son una forma de representar razones entre dos cantidades. La fracción muestra cómo una cantidad se compara con otra en términos de partes iguales.