Ángulos entre paralelas y una transversal

Ángulos entre paralelas cortadas por una transversal

Los ángulos entre paralelas son aquellos que se forman cuando dos líneas paralelas son cortadas (intersectadas) por una tercera línea, conocida como transversal. Al cortar dos rectas paralelas con una transversal, se generan ocho ángulos.

En la siguiente imagen, \(L_1\) y \(L_2\) son líneas paralelas y \(L_3\) es la línea transversal. Los valores de \(a\), \(b\), \(c\), \(d\), \(p\), \(q\), \(r\) y \(s\) representan los ángulos generados.

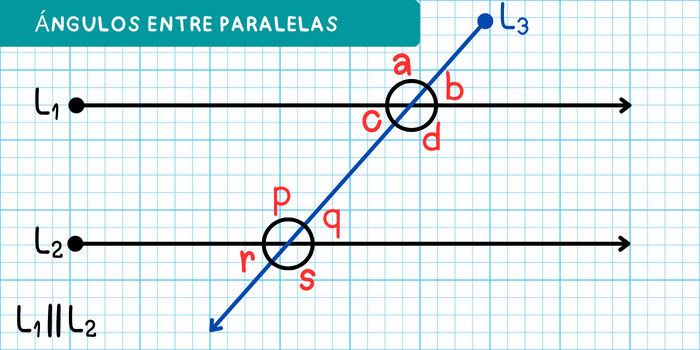
Los tipos de ángulos que se forman cuando dos líneas paralelas son cortadas por una transversal son:

• Ángulos correspondientes.
• Ángulos alternos internos.
• Ángulos alternos externos.
• Ángulos opuestos por el vértice.
• Ángulos colaterales.

Ángulos correspondientes

Los ángulos correspondientes son un tipo de ángulos que se forman cuando dos líneas paralelas son intersectadas por una línea transversal. Estos ángulos se encuentran en el mismo lado de la recta transversal, están al mismo nivel respecto a la recta paralela y tienen la misma magnitud.

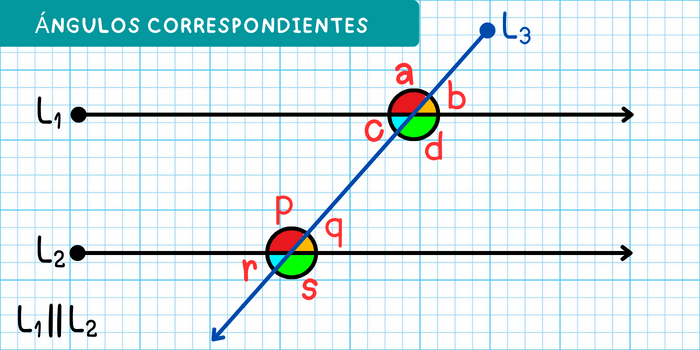
En la figura, los pares de ángulos correspondientes son:

• El ángulo \(a\) es correspondiente al ángulo \(p\).
• El ángulo \(b\) es correspondiente al ángulo \(q\).
• El ángulo \(c\) es correspondiente al ángulo \(r\).
• El ángulo \(d\) es correspondiente al ángulo \(s\).

Como los ángulos correspondientes formados por dos rectas paralelas son congruentes (iguales), entonces:

• El ángulo \(a\) es igual al ángulo \(p\).
• El ángulo \(b\) es igual al ángulo \(q\).
• El ángulo \(c\) es igual al ángulo \(r\).
• El ángulo \(d\) es igual al ángulo \(s\).

Ángulos correspondientes ejercicios resueltos

Ejercicio 1. De la siguiente figura, ¿Cuál es el valor de \(x\)?

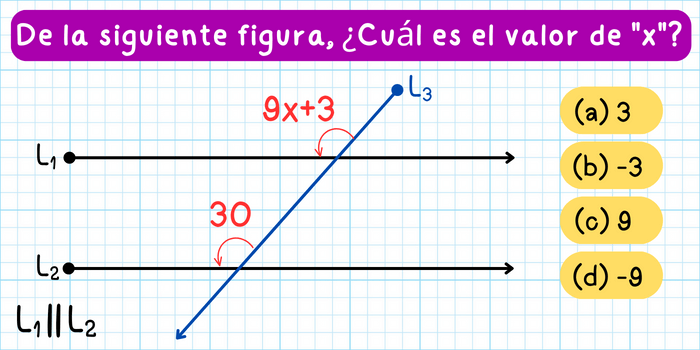
Solución: Observa que los ángulos en la figura son ángulos correspondientes, como estos ángulos son congruentes, es decir, son iguales, entonces se cumple la siguiente igualdad: \[9x+3=30\] Resolviendo esta ecuación, obtenemos que: \[\begin{aligned}9x+3&=30\\9x&=30-3\\9x&=27\\x&=\frac{27}{9}\\x&=3\end{aligned}\] Concluimos que el valor de \(x\) en la figura es \(x=3\).

Ángulos alternos internos

Los ángulos alternos internos son los ángulos que se encuentran en el interior del espacio limitado por las rectas paralelas y la transversal, y se ubican en lados opuestos de la recta transversal. Estos ángulos son congruentes, es decir, tienen la misma magnitud.

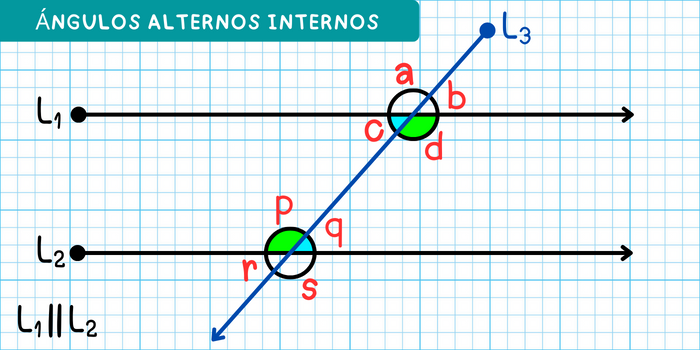
En la figura, los ángulos internos son: \(c\), \(d\), \(p\) y \(q\), de los cuales se cumple que:

• Los ángulos \(c\) y \(q\) son alternos internos.
• Los ángulos \(d\) y \(p\) son alternos internos.

Como los ángulos alternos internos son congruentes (iguales), entonces:

• Los ángulos \(c\) y \(q\) son iguales.
• Los ángulos \(d\) y \(p\) son iguales.

Nota 1. Los ángulos internos consecutivos son suplementarios, es decir, suman 180°.

Ángulos alternos internos ejercicios resueltos

Ejercicio 2. De la siguiente figura, ¿Cuál es el valor de \(y\)?

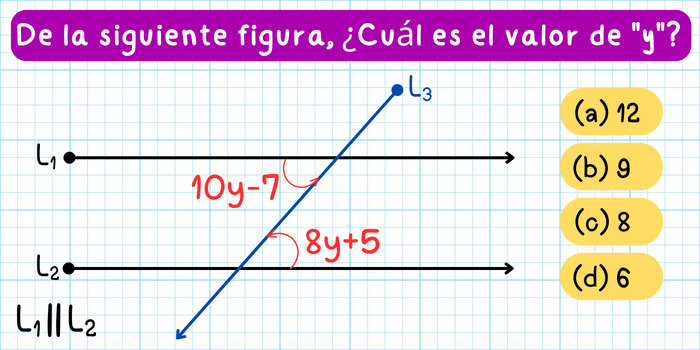
Solución: Observa que los ángulos en la figura son ángulos alternos internos. Como los ángulos alternos internos son congruentes, es decir, son iguales, entonces se cumple la siguiente igualdad: \[10y-7=8y+5\] Resolviendo esta ecuación, obtenemos que: \[\begin{aligned}10y-7&=8y+5\\10y-8y&=5+7\\2y&=12\\x&=\frac{12}{2}\\y&=6\end{aligned}\] Concluimos que el valor de \(y\) en la figura es \(y=6\).

Ángulos alternos externos

Los ángulos alternos externos son los ángulos que se encuentran en el exterior del espacio limitado por las rectas paralelas y la transversal, y estos se ubican en lados opuestos de la recta transversal. Estos ángulos son congruentes, es decir, tienen la misma medida.

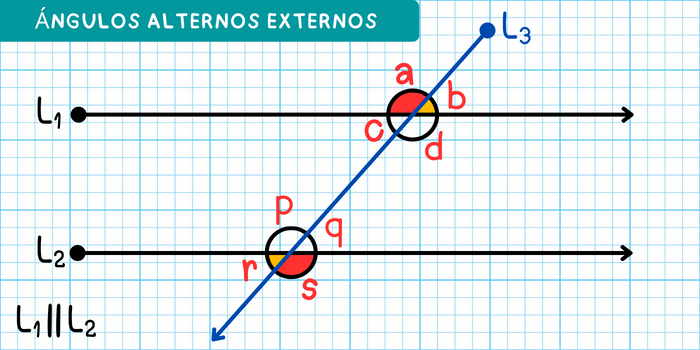
En la figura, los ángulos externos son: \(a\), \(b\), \(r\) y \(s\), de los cuales se cumple que:

• Los ángulos \(a\) y \(s\) son alternos externos.
• Los ángulos \(b\) y \(r\) son alternos externos.

Como los ángulos alternos externos son congruentes (iguales), entonces:

• Los ángulos \(a\) y \(s\) son iguales.
• Los ángulos \(b\) y \(r\) son iguales.

Nota 2. Los ángulos externos consecutivos son suplementarios, es decir, la suma de sus valores es igual a 180°.

Ángulos alternos externos ejercicios resueltos

Ejercicio 3. De la siguiente figura, ¿Cuál es el valor de \(z\)?

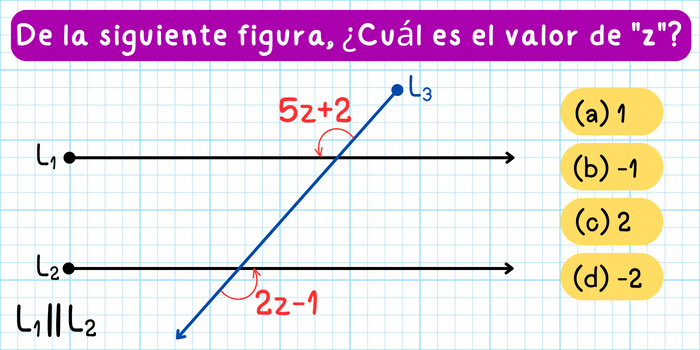
Solución: Observa que los ángulos en la figura son ángulos alternos externos. Como los ángulos alternos externos son congruentes, es decir, son iguales, entonces se cumple la siguiente igualdad: \[5z+2=2z-1\] Resolviendo esta ecuación, obtenemos: \[\begin{aligned}5z+2&=2z-1\\5z-2z&=-1-2\\3z&=-3\\z&=\frac{-3}{3}\\z&=-1\end{aligned}\] Concluimos que el valor de \(z\) en la figura es \(z=-1\).

Ángulos opuestos por el vértice

Los ángulos opuestos por el vértice son aquellos que comparten un vértice común y se ubican en lados opuestos de una intersección de dos rectas. La característica clave de los ángulos opuestos por el vértice es que tienen la misma medida. Esto significa que si conoces el valor de uno de los ángulos, automáticamente sabrás el valor del otro ángulo.

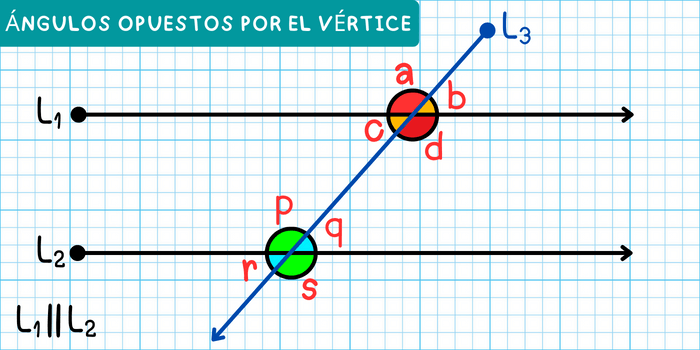
En la figura, todos los pares de ángulos opuestos por el vértice son:

• Los ángulos \(a\) y \(d\).
• Los ángulos \(b\) y \(c\).
• Los ángulos \(p\) y \(s\).
• Los ángulos \(q\) y \(r\).

Como los ángulos opuestos por el vértice son iguales, entonces se cumple que:

• Los ángulos \(a\) y \(d\) son iguales.
• Los ángulos \(b\) y \(c\) son iguales.
• Los ángulos \(p\) y \(s\) son iguales.
• Los ángulos \(q\) y \(r\) son iguales.

Ángulos opuestos por el vértice ejercicios resueltos

Ejercicio 4. De la siguiente figura, ¿Cuál es el valor de \(x\)?

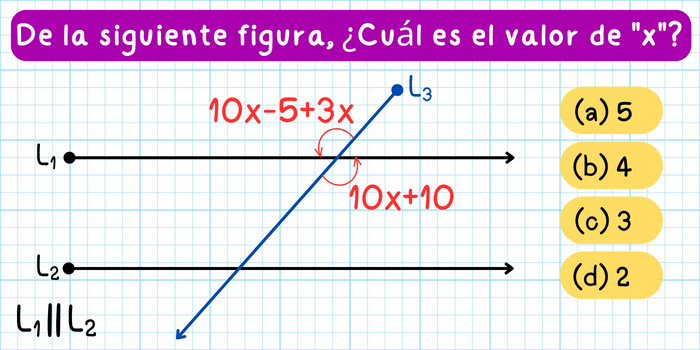
Solución: Observa que los ángulos en la figura son ángulos opuestos por el vértice. Dado que estos ángulos son iguales, se cumple la siguiente igualdad: \[10x-5+3x=10x+10\] Resolviendo esta ecuación, obtenemos: \[\begin{aligned}10x-5+3x&=10x+10\\13x-5&=10x+10\\13x-10x&=10+5\\3x&=15\\x&=\frac{15}{3}\\x&=5\end{aligned}\] Concluimos que el valor de \(x\) en la figura es \(x=5\).

Ángulos colaterales

Los ángulos colaterales son aquellos que se encuentran en el mismo lado de una línea transversal. Los ángulos colaterales son suplementarios, es decir la suma de sus magnitudes es igual a 180°. Los ángulos colaterales pueden ser colaterales internos o colaterales externos.

• Los ángulos colaterales internos son aquellos que se encuentran en el interior de las líneas paralelas y en el mismo lado de la línea transversal.
• Los ángulos colaterales externos son aquellos que se encuentran en el exterior de las líneas paralelas y en el mismo lado de la línea transversal.

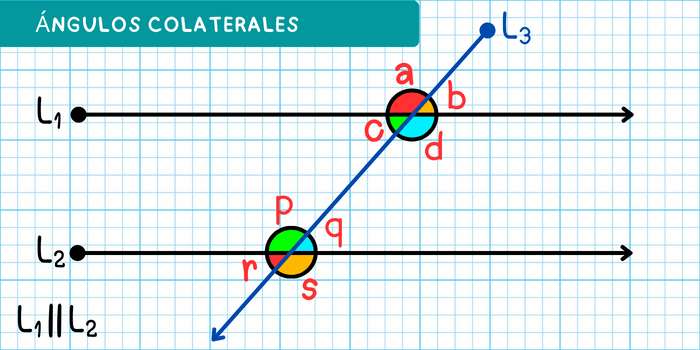
En la figura, todos los pares de ángulos colaterales internos son:

• Los ángulos \(c\) y \(p\).
• Los ángulos \(d\) y \(q\).

Y todos los pares de ángulos colaterales externos son:

• Los ángulos \(a\) y \(r\).
• Los ángulos \(b\) y \(s\).

Ángulos entre paralelas ejercicios resueltos

Ejercicio 5. De la siguiente figura calcular el valor del ángulo \(2x+10\).

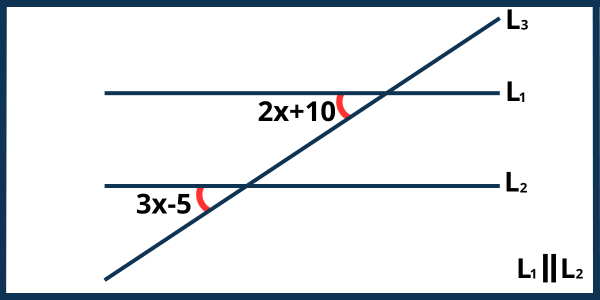
Solución. Observa que los ángulos en la figura son ángulos correspondientes. Recuerda que los ángulos correspondientes son aquellos que se encuentran en el mismo lado de la recta transversal, están al mismo nivel respecto a la recta paralela y tienen la misma magnitud. Dado que los ángulos de la figura son correspondientes, tienen la misma medida, lo que lleva a la siguiente igualdad: \[2x+10=3x-5\] De esta igualdad despejamos el valor de \(x\): \[\begin{aligned}2x+10&=3x-5\\2x-3x&=-5-10\\-x&=-15\\x&=15\end{aligned}\] Ahora que conocemos el valor de \(x\), simplemente lo sustituimos en la expresión del ángulo que queremos hallar. Para encontrar el valor del ángulo \(2x+10\): \[\begin{aligned}2x+10&=2(15)+10\\&=30+10\\&=40\end{aligned}\] De esta manera, el valor del ángulo \(2x+10\) es de 40°.

Ejercicio 6. Observa la figura siguiente y calcula el valor del ángulo \(5x+7\).

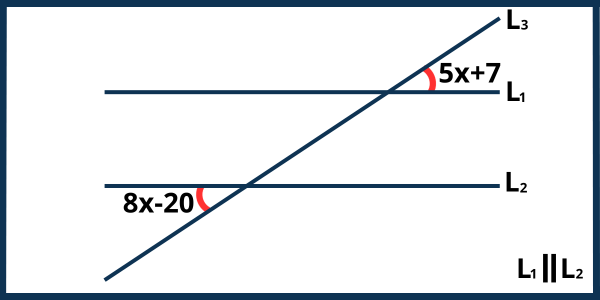
Solución. En este caso, observa que los ángulos en la figura son ángulos alternos externos. Recuerda que los ángulos alternos externos son aquellos que se encuentran en el exterior del espacio limitado por las rectas paralelas. Se ubican en lados opuestos de la recta transversal y son congruentes, es decir, tienen la misma medida. Dado que los ángulos de la figura son alternos externos, tienen la misma medida, lo que nos lleva a la siguiente igualdad: \[5x+7=8x-20\] Al resolver esta igualdad para \(x\), obtenemos: \[\begin{aligned}5x+7&=8x-20\\5x-8x&=-20-7\\-3x&=-27\\3x&=27\\x&=\frac{27}{3}\\x&=9\end{aligned}\] Ahora que conocemos el valor de \(x\), simplemente lo sustituimos en la expresión del ángulo que queremos hallar. Para encontrar el valor del ángulo \(5x+7\): \[\begin{aligned}5x+7&=5(9)+7\\&=45+7\\&=52\end{aligned}\] De esta manera, el valor del ángulo \(5x+7\) es de 52°.

Ejercicio 7. De la siguiente figura hallar el valor del ángulo \(12x-14\).

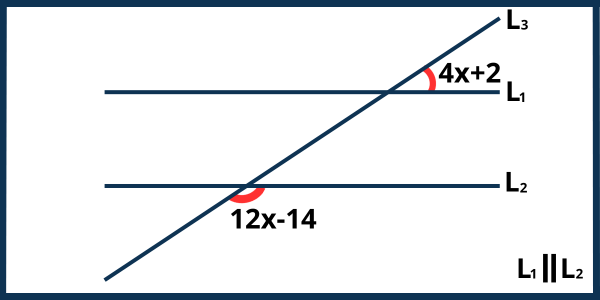
Solución. Los ángulos en la figura son ángulos colaterales externos. Recuerda que los ángulos colaterales externos se encuentran en el exterior de las líneas paralelas, en el mismo lado de la línea transversal y son suplementarios (suman 180°). Dado que los ángulos en la figura son colaterales externos, su suma es igual a 180°, es decir:

\[(4x+2)+(12x-14)=180\]

Resolviendo esta ecuación para \(x\), obtenemos:

\[\begin{aligned}(4x+2)+(12x-14)&=180\\4x+12x+2-14&=180\\16x-12&=180\\16x&=180+12\\x&=\frac{192}{16}\\x&=12\end{aligned}\]

Ahora que conocemos el valor de \(x\), simplemente sustituimos su valor en la expresión del ángulo que queremos hallar. Para encontrar el valor del ángulo \(12x-14\): \[\begin{aligned}12x-14&=12(12)-14\\&=144-14\\&=130\end{aligned}\] De esta manera, el valor del ángulo \(12x-14\) es 130°.

Ejercicio 8. De la siguiente figura obtener el valor del ángulo \(X\).

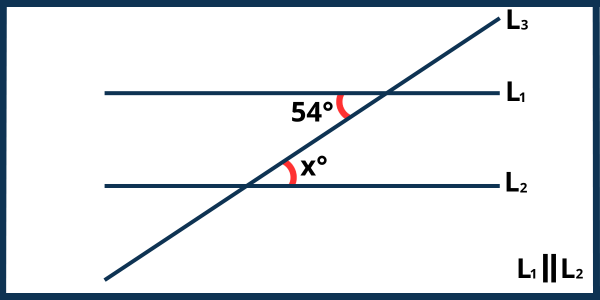
Solución. Observa que los ángulos en la figura son ángulos alternos internos. Como los ángulos alternos internos son congruentes, es decir, tienen la misma medida, entonces se cumple la siguiente igualdad: \[x=54°\] Por lo tanto, el valor del ángulo \(x\) es de 64°.

Ejercicio 9. Hallar el valor del ángulo \(2x-2\).

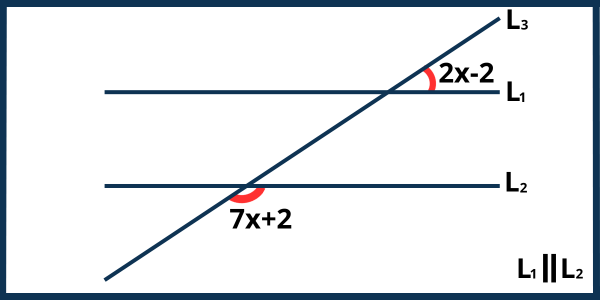
Solución. Observa que los ángulos en la figura son colaterales externos. Los ángulos colaterales externos son aquellos que se encuentran en el exterior de las líneas paralelas, en el mismo lado de la línea transversal y son suplementarios, es decir, su suma es igual a 180°. Con esta información, planteamos la siguiente igualdad:

\[(2x-2)+(7x+2)=180\]

Resolviendo esta ecuación para \(x\), obtenemos lo siguiente:

\[\begin{aligned}(2x-2)+(7x+2)&=180\\2x+7x+2-2&=180\\9x+0&=180\\9x&=180\\x&=\frac{180}{9}\\x&=20\end{aligned}\]

Ahora que conocemos el valor de \(x\), simplemente sustituimos su valor en la expresión del ángulo que queremos hallar. Para encontrar el valor del ángulo \(2x-2\), realizamos lo siguiente: \[\begin{aligned}2x-2&=2(20)-2\\&=40-2\\&=38\end{aligned}\] De esta manera, el valor del ángulo \(2x-2\) es de 38°.

Preguntas frecuentes

¿Qué son los ángulos entre paralelas? Los ángulos entre paralelas son los ángulos formados cuando una línea transversal corta dos líneas paralelas. Estos ángulos tienen propiedades especiales debido a su relación con las líneas paralelas.

¿Cuántos ángulos se forman al cortar dos líneas paralelas con una línea transversal? Cuando se cortan dos líneas paralelas con una línea transversal, se forman ocho ángulos. Estos ángulos se distribuyen en cuatro pares, y cada par consta de dos ángulos congruentes. Los tipos de ángulos que se generan son: ángulos correspondientes, ángulos alternos internos, ángulos alternos externos y ángulos colaterales.

¿Qué son los ángulos correspondientes? Los ángulos correspondientes son pares de ángulos que se encuentran del mismo lado de la recta transversal que corta dos rectas paralelas y están en el mismo nivel respecto a la recta paralela. Los ángulos correspondientes son congruentes, es decir, tienen la misma medida.

¿Qué son los ángulos alternos internos? Los ángulos alternos internos son pares de ángulos que se sitúan en lados opuestos de la línea transversal y entre las líneas paralelas. Estos ángulos son congruentes, es decir, tienen exactamente la misma medida.

¿Qué son los ángulos alternos externos? Los ángulos alternos externos son pares de ángulos que se encuentran en lados opuestos de la línea transversal y fuera de las líneas paralelas. Estos ángulos son congruentes, es decir, tienen la misma medida.

¿Qué son los ángulos colaterales? Los ángulos colaterales son aquellos que se encuentran en el mismo lado de una línea transversal. Los ángulos colaterales pueden ser internos o externos y no necesariamente tienen la misma medida. La propiedad principal de los ángulos colaterales es que su suma siempre es igual a 180 grados.

¿Los ángulos entre paralelas siempre son congruentes? No. No todos los ángulos entre paralelas son congruentes. Solo los ángulos alternos internos y los ángulos alternos externos son congruentes debido a la relación especial entre las líneas paralelas y la transversal.