¿Qué son los ángulos suplementarios?
Los ángulos suplementarios son aquellos que, al sumar sus medidas, dan como resultado un ángulo de 180°. Cuando unimos a dos ángulos suplementarios, se forma una línea recta. En otras palabras, la suma de dos ángulos suplementarios siempre resulta en un ángulo llano (180 grados).
Ángulos suplementarios ejemplos
Existen tres tipos de ángulos suplementarios: ángulos suplementarios adyacentes, ángulos suplementarios no adyacentes y ángulos suplementarios rectos. A continuación, veremos las características, así como ejemplos de cada uno de estos tipos de ángulos suplementarios.
Ángulos suplementarios adyacentes
En primer lugar, es importante recordar que los ángulos adyacentes son aquellos que comparten un vértice y un lado, pero no comparten ningún punto interior. Cuando dos ángulos son adyacentes y suplementarios, significa que están uno al lado del otro (adyacentes) y que la suma de sus medidas es igual a 180 grados (suplementarios). Para que dos ángulos sean considerados suplementarios adyacentes, deben cumplir con las siguientes condiciones: compartir un vértice, compartir un lado común y que la suma de sus medidas sea igual a 180 grados. La siguiente imagen muestra a dos ángulos suplementarios adyacentes.
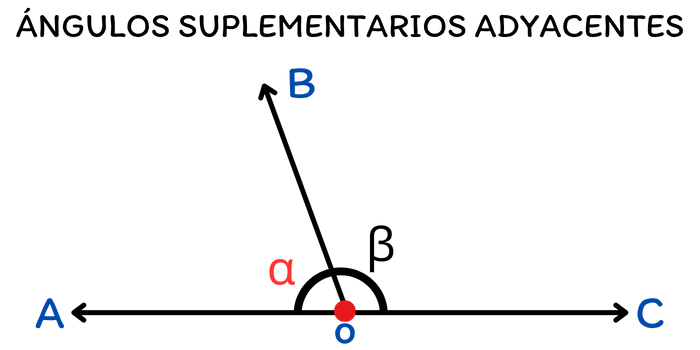
Observa que ambos ángulos comparten el mismo vértice \(O\), comparten el segmento de recta \(OB\), y la suma de sus medidas es igual a 180 grados. Los ángulos suplementarios adyacentes son comunes en geometría y se utilizan para resolver problemas relacionados con líneas rectas y ángulos en diversas situaciones matemáticas y geométricas.
Ángulos suplementarios no adyacentes
Cuando dos ángulos no son adyacentes y suplementarios, significa que estos ángulos no comparten un vértice común ni un lado común. En otras palabras, están separados y no están uno al lado del otro. En contraste con los ángulos suplementarios adyacentes, que comparten un vértice y un lado común, los ángulos suplementarios no adyacentes simplemente cumplen con la condición de que la suma de sus valores es igual a 180 grados. La siguiente imagen muestra a dos ángulos suplementarios no adyacentes.
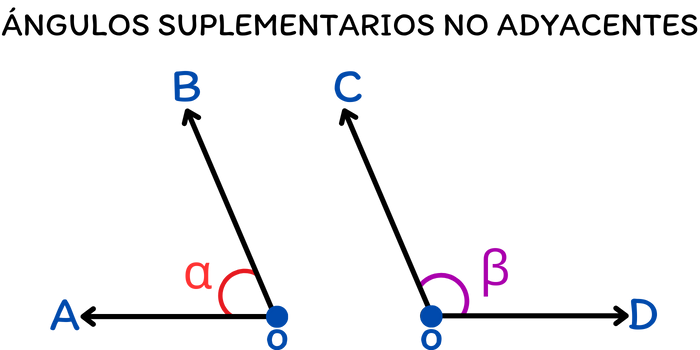
Observa que los ángulos no comparten un vértice común, ni tampoco comparten algún segmento de recta. Sin embargo, estos ángulos sí son suplementarios, ya que la suma de sus valores es igual a 180 grados y forman una línea recta al unirlos. Este concepto es relevante en problemas geométricos y matemáticos donde se requiere encontrar dos ángulos cuya suma sea 180 grados, pero no es necesario que estén uno al lado del otro o compartan un punto común.
Ángulos suplementarios rectos
Los ángulos suplementarios rectos son aquellos que miden entre sí 90 grados. Esto significa que si un ángulo mide 90°, su ángulo suplementario también medirá 90°. La siguiente imagen muestra dos ángulos suplementarios rectos. Estos ángulos pueden ser adyacentes o no adyacentes.
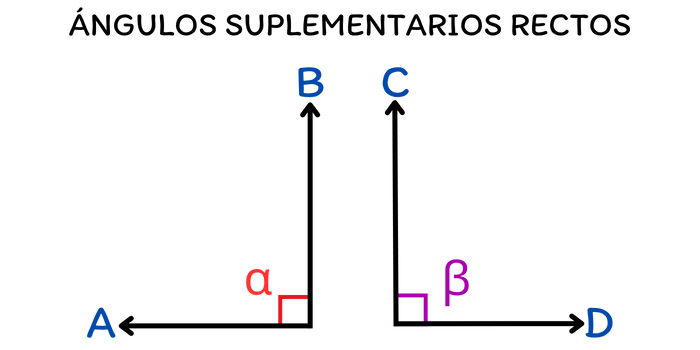
Propiedades de los ángulos suplementarios
Propiedad 1. La suma de dos ángulos suplementarios es igual a 180°. Esta propiedad establece que, si se tienen dos ángulos suplementarios \(\alpha\) y \(\beta\), entonces: \[\alpha+\beta=180°\]
Propiedad 2. Si un ángulo es suplementario a otro, entonces el segundo también es suplementario al primero. Esta propiedad establece que, si por ejemplo tenemos un ángulo \(\alpha\) de 20°, su ángulo suplementario \(\beta\) será de 160°, ya que: \[20°+160°=180°\] y el ángulo suplementario de 160° será el ángulo de 20°, ya que también se cumple que: \[160°+20°=180°\]
Propiedad 3. Si un ángulo es un ángulo recto (90°), entonces su suplemento será otro ángulo recto. Esta propiedad establece que, el ángulo suplementario de un ángulo recto (90°) será otro ángulo recto, ya que: \[90°+90°=180°\]
Propiedad 4. Los ángulos suplementarios pueden ser adyacentes o no adyacentes. Esta propiedad establece que, la condición principal para que dos ángulos sean suplementarios es que sumen 180°, independientemente de si son adyacentes o no.
- Dos ángulos suplementarios son adyacentes si comparten un lado y un vértice común. En otras palabras, se encuentran uno al lado del otro.
- Dos ángulos suplementarios son no adyacentes si no comparten un lado ni un vértice común. Pueden estar separados por otros ángulos o incluso por figuras geométricas.
Propiedad 5. Para que dos ángulos sean suplementarios uno de ellos debe ser agudo y el otro obtuso. Esta propiedad establece que, si \(\alpha\) es un ángulo agudo, es decir, su medida es menor a 90°, entonces su ángulo suplementario \(\beta\) será un ángulo obtuso, es decir, mayor a 90°, y viceversa. Esto significa que si se tiene un ángulo agudo y su suplemento, la suma de ambos será igual a 180 grados, es decir: \[\alpha+\beta=180°\]
Propiedad 6. Los senos de los ángulos suplementarios son los mismos, matemáticamente, si \(\alpha\) es el ángulo suplementario del ángulo \(\beta\), es decir: \[\alpha+\beta=180°\] Entonces, el seno del ángulo suplementario \(\alpha\) es igual al seno del ángulo \(\beta\). Esto significa que: \[\sin{\alpha}=\sin{\beta}\]
Por ejemplo, si el ángulo \(\alpha\) de 120° es el ángulo suplementario del ángulo \(\beta\) de 60°, entonces: \[\begin{aligned}\sin{120°}=\sin{60°}\end{aligned}\]
Propiedad 7. Los cosenos de los ángulos suplementarios son de igual valor absoluto, pero de signo contrario. Es decir, si \(\alpha\) es el ángulo suplementario de \(\beta\), se cumple que: \[\alpha+\beta=180°\] Entonces, el coseno del ángulo suplementario \(\alpha\) es igual a menos el coseno del ángulo \(\beta\). Matemáticamente, esto significa que: \[\cos{\alpha}=-\cos{\beta}\]
Por ejemplo, si el ángulo \(\alpha\) de 30° es el ángulo suplementario del ángulo \(\beta\) de 150°, entonces: \[\begin{aligned}\cos{30°}=-\cos{150°}\end{aligned}\]
¿Cómo encontrar un ángulo suplementario?
Para obtener el ángulo suplementario \(\beta\) de un determinado ángulo \(\alpha\), se debe restar \(\alpha\) a \(180°\), de manera que: \[\beta=180°-\alpha\]
Ángulos suplementarios ejercicios resueltos
Ejercicio 2. En la siguiente figura, ¿Cuál es el valor de \(y\)?
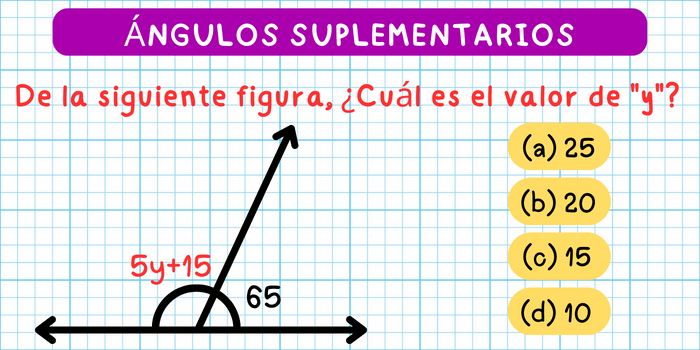
Solución: Observa que, los ángulos indicados en la figura son ángulos suplementarios, por lo tanto se debe cumplir que: \[(5y+15)+65=180\] Esta es una ecuación lineal ( de primer grado), para resolver esta ecuación seguimos los pasos de la regla general para hallar la solución a una ecuación. Así obtenemos que: \[\begin{aligned}(5y+15)+65&=180\\5y+15+65&=180\\5y+80&=180\\5y&=180-80\\5y&=100\\y&=\frac{100}{5}\\y&=20\end{aligned}\] De esta manera \(y=20\) satisface la ecuación que verifica que los ángulos son suplementarios.
¡En resumen!
La próxima vez que estés trabajando con ángulos suplementarios recuerda lo siguiente: Un ángulo es suplementario a otro si la suma de sus medidas es igual a 180°. Los ángulos suplementarios pueden ser adyacentes o no adyacentes. Por lo general se trabaja con ángulos positivos, lo que implica que dos ángulos son suplementarios si uno de ellos es agudo (menor a 90°) y el otro es obtuso (mayor a 90°).