¿Qué es un vector?
Un vector es un segmento de recta que que va del punto \(P\) al punto \(Q\) y se denota comúnmente como \(\vec{PQ}\). Al punto \(P\) se le llama punto inicial u origen del vector y al punto \(Q\) se le llama punto final o punto terminal del vector. La palabra "vector" proviene del latín "vectus", que significa "transportar" o "llevar".
En matemáticas y física, el término "vector" se utiliza para referirse a una entidad que lleva información sobre magnitud y dirección en un espacio determinado. Para diferenciar un vector de un escalar, a un vector se le denota con letras escritas en negrita, o con letras escritas con una flecha encima. De esta manera el vector \(\vec{PQ}\) se puede escribir simplemente como \(\mathbf{A}\) o \(\vec{A}\).
Artículo recomendado: Cantidades escalares y vectoriales
¿Cómo se representan los vectores?
Los vectores se representan de varias formas dependiendo del contexto y la dimensión del espacio en el que operan. A continuación te presentamos las formas más comunes de representar un vector.
Representación gráfica de un vector
En un plano bidimensional o en el espacio tridimensional, los vectores se pueden representar como flechas que comienzan desde un punto de origen y se extienden en una dirección específica con una longitud proporcional a su magnitud. La dirección y el sentido de la flecha indican la dirección y el sentido del vector, mientras que la longitud de la flecha representa su magnitud.
Vector en dos dimensiones
Un vector \(\vec{A}\) en dos dimensiones puede representarse con su punto inicial en el origen \(O=(0, 0)\) y su punto final en cualquier otro punto, digamos en \((A_1, A_2)\), de tal manera que podemos escribir al vector \(\vec{A}\) como: \[\vec{A}=A_1\mathbf{i}+A_2\mathbf{j}\] Los vectores \(A_1\mathbf{i}\) y \(A_2 \mathbf{i}\) se denominan vectores componentes de \(\vec{A}\) en las direcciones \(x\) y \(y\). Los escalares \(A_1\) y \(A_2\) se les denomina componentes de \(\vec{A}\) en las direcciones \(x\) y \(y\).
Vector en tres dimensiones
Un vector \(\vec{B}\) en tres dimensiones puede representarse con su punto inicial en el origen \(O=(0, 0, 0)\) y su punto final en cualquier otro punto, digamos en \((B_1, B_2, B_3)\), de tal manera que podemos escribir al vector \(\vec{B}\) como: \[\vec{B}=B_1\mathbf{i}+B_2\mathbf{j}+B_3\mathbf{k}\] Los vectores \(B_1\mathbf{i}\), \(B_2 \mathbf{j}\) y \(B_3\mathbf{k}\) se denominan vectores componentes de \(\vec{B}\) en las direcciones \(x\), \(y\) y \(z\). Los escalares \(B_1\), \(B_2\) y \(B_3\) se les denomina componentes de \(\vec{B}\) en las direcciones \(x\), \(y\) y \(z\).
¿Cuáles son las características de un vector?
Los vectores tienen varias características importantes que los definen y los distinguen de otras entidades matemáticas. A continuación te presentamos las características más importantes de los vectores.
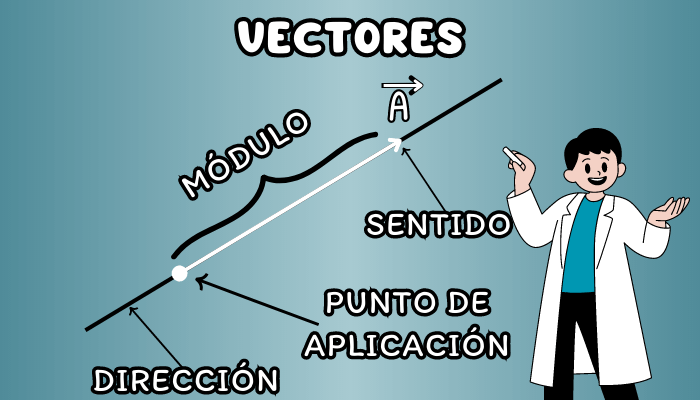
Módulo, magnitud o longitud de un vector
Cada vector tiene una magnitud o longitud que representa la cantidad de la propiedad que está siendo medida. La magnitud se representa numéricamente y es siempre un número real no negativo. De forma general el módulo, magnitud o longitud de un vector \(\vec{A}\) se denota como: \[|\vec{A}|=A\] Para un vector \(\vec{A}\) en dos dimensiones, la longitud se obtiene simplemente calculando la raíz cuadrada de la suma de los cuadrados de las dos componentes, es decir; \[\begin{aligned}|\vec{A}|=\sqrt{A_{1}^2+A_{2}^2}\end{aligned}\] Para un vector \(\vec{B}\) en tres dimensiones, la longitud se obtiene simplemente calculando la raíz cuadrada de la suma de los cuadrados de las tres componentes, es decir; \[\begin{aligned}|\vec{B}|=\sqrt{B_{1}^2+B_{2}^2+B_{3}^2}\end{aligned}\]
Dirección de un vector
La dirección de un vector es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella. Para un vector \(\vec{A}\) en dos dimensiones la dirección se puede determinar de la siguiente manera: \[\theta=\tan^{-1}\left(\frac{A_2}{A_1}\right)\]
Sentido de un vector
Los vectores también tienen un sentido, que indica si el vector se está moviendo en una dirección positiva o negativa en relación con el eje de referencia. El sentido de un vector viene representado por la punta de la flecha que se expresa gráficamente, indicando el lugar hacia el cual se dirige el vector.
Representación gráfica de un vector
Los vectores se suelen representar gráficamente como flechas en un plano o en un espacio tridimensional. La longitud de la flecha representa la magnitud del vector, y la dirección y el sentido de la flecha representan la dirección y el sentido del vector. (Magnitud, dirección y sentido de un vector)
Punto de aplicación (solo para vectores ligados)
En algunos contextos, como en el estudio de fuerzas en física, los vectores pueden tener un punto de aplicación, que es el punto desde el cual se origina el vector. Esto es especialmente relevante para los vectores ligados, ya que su dirección y magnitud pueden cambiar si se desplazan en el espacio.
Álgebra de vectores
Los vectores pueden someterse a varias operaciones matemáticas, como la suma de vectores, la resta de vectores, la multiplicación de un vector por un escalar, el producto punto de vectores (producto escalar) y el producto cruz de vectores (en espacios tridimensionales).
¿Qué tipo de vectores existen?
Los vectores se pueden clasificar en diferentes tipos según sus propiedades y características específicas. A continuación te presentamos los vectores más comunes.
Vector unitario
Un vector unitario es aquel que tiene magnitud igual a la unidad. Se utilizan a menudo para describir direcciones en el espacio. En un espacio tridimensional, los vectores unitarios \(\mathbf{i}\), \(\mathbf{j}\) y \(\mathbf{k}\) son aquellos que apuntan en las direcciones positivas de los ejes \(x\), \(y\) y \(z\), respectivamente.
Vector nulo o vector cero
El vector nulo o vector cero es aquel que tiene todas sus componentes iguales a cero. El vector nulo no tiene magnitud ni dirección y se denota como \(\vec{0}\)
Vectores paralelos
Un vector es paralelo a otro cuando sus coordenadas son proporcionales, es decir, los vectores paralelos son aquellos que tienen la misma dirección. Aunque estos vectores pueden tener diferentes magnitudes, su dirección es la misma.
Vectores perpendiculares
Los vectores perpendiculares son aquellos que son mutuamente perpendiculares, lo que significa que forman un ángulo de \(90°\) entre sí.
Vectores colineales
Los vectores colineales son aquellos que aparecen en la misma recta o que resultan ser paralelos a una cierta recta.
Vectores libres
Los vectores libres son aquellos que están completamente definidos por su magnitud y dirección, independientemente de su punto de aplicación en el espacio. Es decir, su punto de aplicación es libre (puede estar en cualquier parte) o simplemente no está definido.
Vectores ligados o vectores de desplazamiento
Los vectores ligados o vectores de desplazamiento son aquellos que tienen un punto de aplicación específico en el espacio y representan el desplazamiento entre dos puntos. Su magnitud y dirección son independientes de su punto de aplicación.
Vectores coordinados
Los vectores coordinados son aquellos que representan las coordenadas de un punto en un espacio. Por ejemplo, en un espacio bidimensional, el vector de coordenadas \((x, y)\) representa la posición del punto en los ejes \(x\) e \(y\).
Vectores antiparalelos
Los vectores antiparalelos son aquellos que tienen la misma magnitud pero direcciones opuestas, es decir, forman un ángulo de 180 grados entre sí. En otras palabras los vectores antiparalelos van en la misma dirección (línea imaginaria en el espacio) pero en sentido opuesto sobre esa misma dirección.
Vectores unitarios ortogonales
Los vectores unitarios ortogonales son vectores unitarios que son ortogonales entre sí, lo que significa que son perpendiculares y tienen una magnitud de 1.
Vectores propios
En el contexto de álgebra lineal, los vectores propios (también conocidos como eigenvectores) son aquellos que solo cambian en magnitud (no en dirección) cuando se multiplica por una matriz.
¿Cuál es la diferencia entre las magnitudes vectoriales y las de escalares?
Magnitudes escalares
Las magnitudes escalares son cantidades que solo tienen magnitud numérica y no tienen dirección ni sentido asociado. Representan cantidades que se describen completamente con un solo número y una unidad de medida. Ejemplos de magnitudes escalares incluyen la masa (ejemplo correcto), el tiempo (ejemplo correcto), la temperatura (ejemplo correcto), la energía (ejemplo correcto), la velocidad escalar (magnitud de la velocidad) (ejemplo incorrecto, la velocidad es en realidad una magnitud vectorial) y la densidad (ejemplo correcto).
Magnitudes Vectoriales
Las magnitudes vectoriales son cantidades que tienen tanto magnitud numérica como dirección y sentido asociados. Representan cantidades que involucran movimiento o desplazamiento en un espacio. Ejemplos de magnitudes vectoriales incluyen la velocidad (ejemplo correcto), la fuerza (ejemplo correcto), el desplazamiento (ejemplo correcto), la aceleración (ejemplo correcto), el impulso (ejemplo correcto) y el momento angular (ejemplo correcto).