Suma de Vectores
Imagina que estás navegando en un barco en medio de un lago. El viento sopla desde el norte con cierta fuerza y el agua fluye desde el este con otra fuerza. ¿Cómo combinarías estas dos fuerzas para determinar la dirección y magnitud resultante que afecta el movimiento de tu barco?
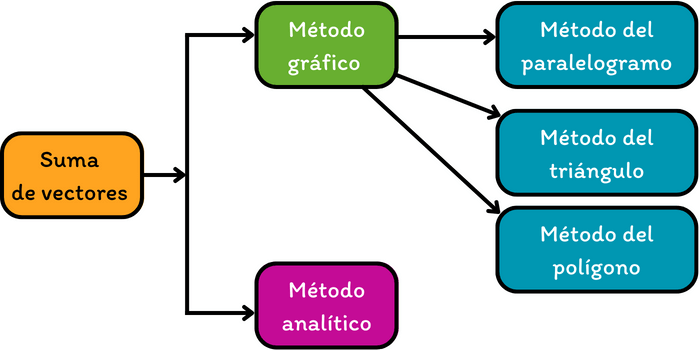
¿Qué es la suma de vectores?
La suma de vectores es una operación que nos permite combinar dos o más vectores individuales en un único vector conocido como vector resultante.
Este concepto es fundamental en la resolución de problemas en física, ingeniería y muchas otras disciplinas. La suma de vectores no solo implica sumar las magnitudes, sino también considerar las direcciones.
En esta entrada, aprenderás a sumar vectores de dos maneras completamente distintas: gráficamente, utilizando métodos visuales, y analíticamente, descomponiendo los vectores en sus componentes individuales. Además, comprenderás las propiedades fundamentales de la suma de vectores que nos permiten manipularlos de manera efectiva y entender su comportamiento en diversos contextos.
Artículo recomendado: Producto punto de vectores: Propiedades y ejemplos
Propiedades de la suma de vectores
Las propiedades de la suma de vectores son reglas que se aplican cuando se requiere sumar dos o más vectores. Estas propiedades son fundamentales para entender cómo se comportan los vectores al combinarlos y cómo podemos manipularlos de manera efectiva para resolver problemas complejos.
Propiedad conmutativa de la suma de vectores
La suma de vectores es conmutativa, lo que significa que el orden en el que se suman los vectores no afecta el resultado. Matemáticamente, para cualquier par de vectores \(\vec{A}\) y \(\vec{B}\), se cumple: \[\vec{A}+\vec{B}=\vec{B}+\vec{A}\]
Propiedad asociativa de la suma de vectores
La suma de vectores es asociativa, lo que significa que podemos agrupar los vectores de diferente manera al realizar la suma y el resultado será el mismo. Matemáticamente, para vectores \(\vec{A}\), \(\vec{B}\) y \(\vec{C}\), se cumple: \[\left(\vec{A}+\vec{B}\right)+\vec{C}=\vec{A}+\left(\vec{B}+\vec{C}\right)\]
Propiedad del neutro aditivo
Existe un vector especial llamado vector cero que se denota como: \(\vec{0}\). Sumar cualquier vector al vector cero resulta en el mismo vector original. Matemáticamente, para cualquier vector \(\vec{A}\), se cumple: \[\vec{A}+\vec{0}=\vec{A}\]
Propiedad del inverso aditivo
Cada vector tiene un vector opuesto o inverso aditivo que, al sumarse, da como resultado el vector cero. El vector opuesto de \(\vec{A}\) se denota como \(-\vec{A}\), y su suma con \(\vec{A}\) resulta en el vector cero. Matemáticamente, se cumple que: \[\vec{A}+\left(-\vec{A}\right)=\vec{0}\]
Propiedad de la multiplicación por un escalar
Podemos multiplicar un vector por un escalar para cambiar su magnitud y dirección. Matemáticamente, para un vector \(\vec{A}\) y un escalar \(k\) se cumple: \[k\cdot \vec{A}=\vec{B}\]
Propiedad distributiva de la suma de vectores
La suma de vectores es distributiva respecto a la multiplicación por un escalar. Matemáticamente, para vectores \(\vec{A}\) y \(\vec{B}\) y \(k\) un escalar, se cumple: \[k\cdot\left(\vec{A}+\vec{B}\right)=k\cdot\vec{A}+k\cdot\vec{B}\]
Propiedad transitiva en la suma de vectores
Si dos vectores son iguales, sus sumas con un tercer vector también serán iguales. Matemáticamente, si \(\vec{A}=\vec{B}\), entonces para cualquier vector \(\vec{C}\) se cumple: \[\vec{A}+\vec{C}=\vec{B}+\vec{C}\]
Artículo recomendado: Producto vectorial: Producto cruz de dos vectores
Suma de vectores método gráfico
El método gráfico para sumar vectores es intuitivo y visualmente impactante. En este enfoque representamos a los vectores como flechas en el plano cartesiano. El método gráfico abarca el método del paralelogramo, el método del triángulo y el método del polígono. A continuación, te presentamos en qué consiste cada uno, así como también los pasos para utilizar estos métodos para sumar dos o más vectores.
Suma de vectores método del paralelogramo
La suma de vectores por el método del paralelogramo consiste en colocar gráficamente los puntos iniciales de los vectores en un punto en común. Luego, al final de cada vector trazar una recta paralela al otro vector. El vector resultante se traza desde el punto de inicio común hasta el punto donde las rectas paralelas a los vectores se cruzan. La longitud y dirección de este vector resultante representa la suma del vector \(\vec{A}\) con el vector \(\vec{B}\). En la siguiente imagen, el vector \(\vec{A}\) representa el primer vector, mientras que \(\vec{B}\) representa al segundo vector.
Paso 1. Identificar a los vectores \(\vec{A}\) y \(\vec{B}\) en el plano cartesiano.
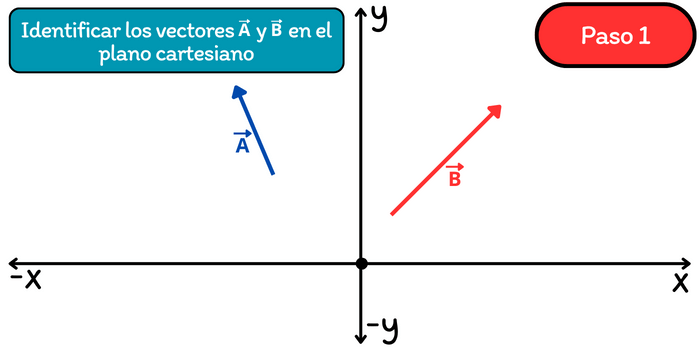
Paso 2. Colocar a los vectores \(\vec{A}\) y \(\vec{B}\) con su punto inicial en un mismo punto. Por lo general se elige al origen de coordenadas como el punto de inicio en común.
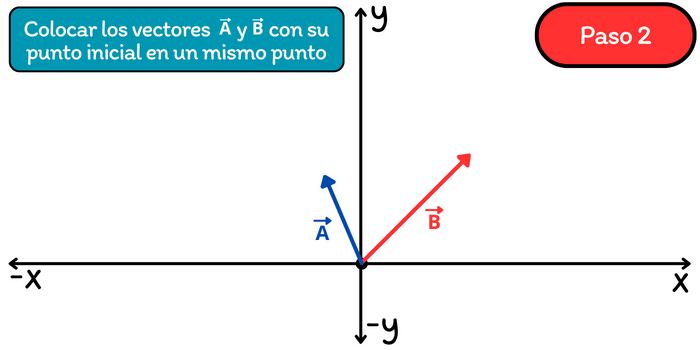
Paso 3. Al final de cada vector trazar una recta paralela al otro vector, justo como se muestra en la siguiente imagen.
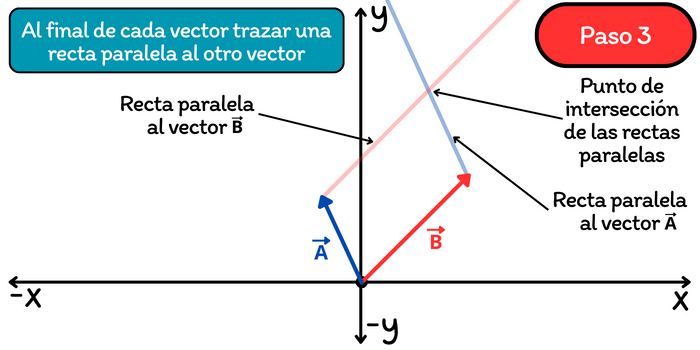
Paso 4. Trazar el vector resultante desde el punto de inicio común hasta el punto donde se intersectan las rectas paralelas trazadas en el paso 3. La longitud y dirección del vector resultante representa la suma del vector \(\vec{A}\) con el vector \(\vec{B}\).
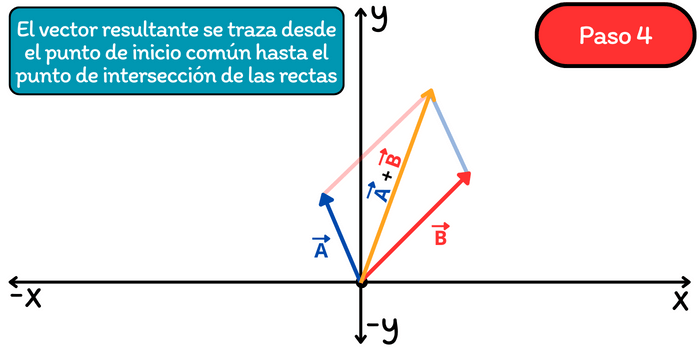
Este método visual nos ayuda a comprender cómo se combinan las magnitudes y direcciones de los vectores al sumarlos. Al trazar las rectas paralelas, creamos un paralelogramo imaginario que nos permite determinar fácilmente el vector resultante. Recuerda que un paralelogramo es una figura geométrica, con la característica de tener sus lados opuestos paralelos y de la misma magnitud.
Suma de vectores método del triángulo
La suma de vectores por el método del triángulo consiste en colocar gráficamente un vector a continuación de otro, es decir, colocar el punto inicial del segundo vector en el punto final del primer vector. El resultado de esta acción es un nuevo vector, el cual representa la suma de los dos vectores iniciales y se traza desde el punto inicial del primer vector hasta el punto final del segundo vector, completando así un triángulo. En la siguiente imagen, el vector \(\vec{A}\) representa el primer vector, mientras que \(\vec{B}\) representa el segundo vector. La longitud y dirección del vector resultante \(\vec{C}\) representa la suma del vector \(\vec{A}\) con el vector \(\vec{B}\).
Paso 1. Identificar a los vectores \(\vec{A}\) y \(\vec{B}\) en el plano cartesiano.
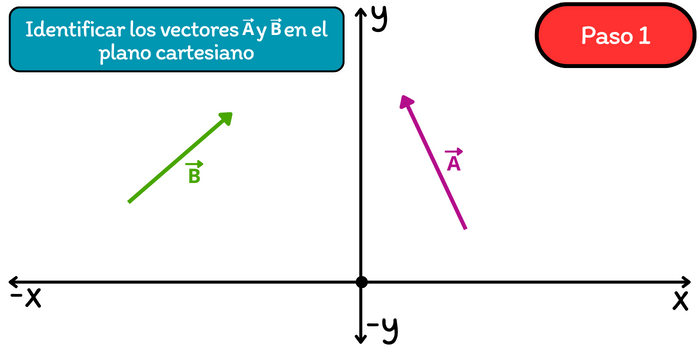
Paso 2. Trasladar el segundo vector (vector \(\vec{B}\)) de tal manera que su punto inicial coincida con en el punto final del primer vector (vector \(\vec{A}\)), justo como se muestra en la siguiente imagen.
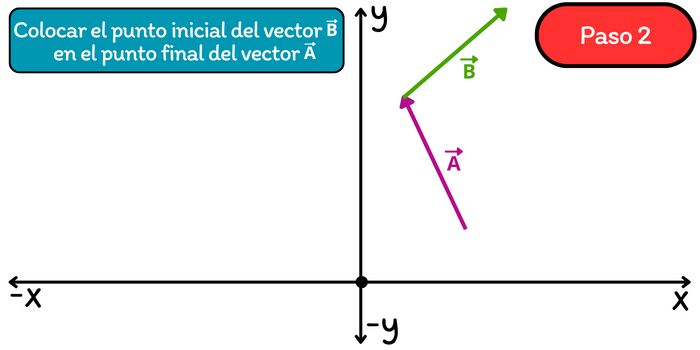
Paso 3. Trazar el vector resultante desde el punto de inicio del vector \(\vec{A}\) hasta el punto final del vector \(\vec{B}\). La longitud y dirección de este vector resultante representa la suma del vector \(\vec{A}\) con el vector \(\vec{B}\).

Este enfoque es particularmente útil para entender cómo se combinan las magnitudes y direcciones de los vectores al sumarlos. Visualizar el proceso a través de un triángulo nos permite captar de manera más clara cómo interactúan los vectores en la suma.
Suma de vectores método del polígono
El método del polígono es otro enfoque utilizado para sumar vectores y es una extensión del método del triángulo y la regla del paralelogramo. Este método es especialmente útil cuando se requiere sumar más de dos vectores. La suma de vectores por el método del polígono consiste en colocar gráficamente los puntos iniciales de todos los vectores en un punto en común. Luego, manteniendo el orden, trasladamos cada vector de tal manera que el punto final de cada vector coincida con el punto inicial del siguiente vector. El vector resultante representa la suma de todos los vectores y se traza desde el punto inicial del primer vector hasta el punto final del último vector.
Paso 1. Identificar los vectores en el plano cartesiano. Recuerda que el método del polígono se utiliza para realizar la suma de dos o más vectores. En este caso, representaremos la suma de cuatro vectores en el plano cartesiano mediante los vectores \(\vec{A}\), \(\vec{B}\), \(\vec{C}\) y \(\vec{D}\).
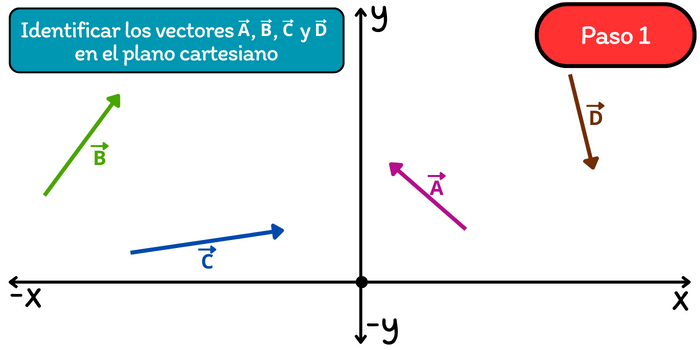
Paso 2. Trasladar a cada uno de los vectores de tal manera que su punto inicial coincida en un mismo punto. Por lo general se elige al origen de coordenadas como el punto de inicio en común.
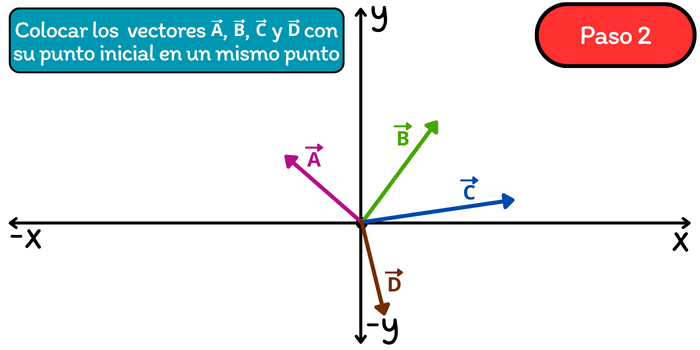
Paso 3. Manteniendo el orden en el que se dan los vectores, trasladar cada uno de tal manera que el punto inicial coincida con punto final del vector anterior.
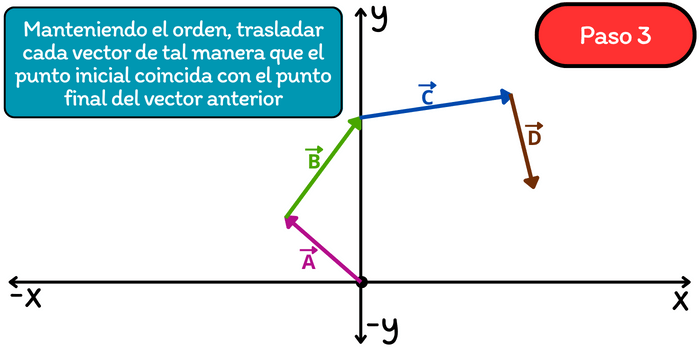
Paso 4. Trazar el vector resultante desde el punto de inicio del primer vector (vector \(\vec{A}\)) hasta el punto final del último vector (\(\vec{D}\)). La longitud y dirección de este vector resultante representa la suma del vector \(\vec{A}\) con el vector \(\vec{B}\) con el vector \(\vec{C}\) con el vector \(\vec{D}\).
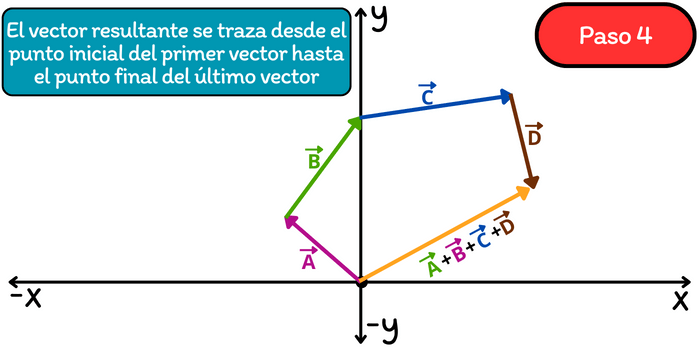
Este método implica sumar los vectores de acuerdo con el orden que se requiere sumar, manteniendo el módulo, la dirección y el sentido. Para este ejemplo se eligió realizar la suma en orden alfabético. Es importante asegurarse de que al aplicar este método, ni dos puntos de inicio ni dos puntos finales deben coincidir en un mismo punto.
Suma de vectores método analítico
Los métodos gráficos nos ayudan a aproximarnos al valor de la resultante de un sistema de vectores y, al mismo tiempo, nos permiten entender cómo se suman estos vectores. Sin embargo, cuando necesitamos conocer el valor exacto de la resultante en un sistema que involucra dos o más vectores, se vuelve necesario recurrir a los métodos analíticos, que incluyen el método del triángulo, el del paralelogramo y el de las componentes rectangulares. A continuación, vamos a examinar cada uno de estos métodos en detalle.
Suma de vectores por el método de las componentes rectangulares
Componentes rectangulares explícitas
Consideremos dos vectores \(\vec{A}\) y \(\vec{B}\) en el plano cartesiano definidos en términos de sus componentes rectangulares: \[\begin{aligned}\vec{A}&=(A_{x}, A_{y})\\\vec{B}&=(B_{x}, B_{y})\end{aligned}\] La suma de vectores mediante el método de las componentes rectangulares implica la adición componente a componente, es decir, si \(\vec{C}\) es el vector resultante que se obtiene de sumar \(\vec{A}\) con \(\vec{B}\), entonces: \[\begin{aligned}\vec{C}&=\vec{A}+\vec{B}\\&=( A_{x}, A_{y})+( B_{x}, B_{y})\\&=(A_{x}+B_{x}, A_{y}+B_{y})\end{aligned}\] De esto se obtiene que las componentes rectangulares del vector resultante son: \[\begin{aligned}\vec{C}&=(C_{x}, C_{y})\\&=( A_{x}+B_{x}, A_{y}+B_{y})\end{aligned}\] La magnitud del vector \(\vec{C}=(C_x, C_y)\) se puede determinar mediante la fórmula: \[|\vec{C}|=\sqrt{(C_{x})^2+(C_y)^2}\] La dirección del vector \(\vec{C}=(C_x, C_y)\) se puede calcular a partir de la siguiente fórmula: \[\theta=\tan^{-1}\left(\frac{C_y}{C_x}\right)\] La expresión \(\theta = \tan^{-1}\left(\frac{C_y}{C_x}\right)\) implica calcular la arcotangente, que es la función inversa de la tangente, del cociente \(C_y/C_x\). Esta operación nos permite determinar la dirección o el ángulo de inclinación del vector resultante. Para obtener el valor del ángulo en grados sexagesimales, es necesario utilizar una calculadora configurada en la función DEG (Degree).
Componentes rectangulares implícitas
Ahora, consideremos un vector \(\vec{C}\) con magnitud \(C\) y ángulo de dirección \(\theta\) con respecto al eje \(x\). Para obtener las componentes rectangulares \((C_x, C_y)\) del vector \(\vec{C}\), nos apoyamos de las identidades trigonométricas del seno y coseno: \[\begin{aligned}\sin{\theta}&=\frac{C. Opuesto}{Hipotenusa}\\\cos{\theta}&=\frac{C. Adyacente }{Hipotenusa}\end{aligned}\]
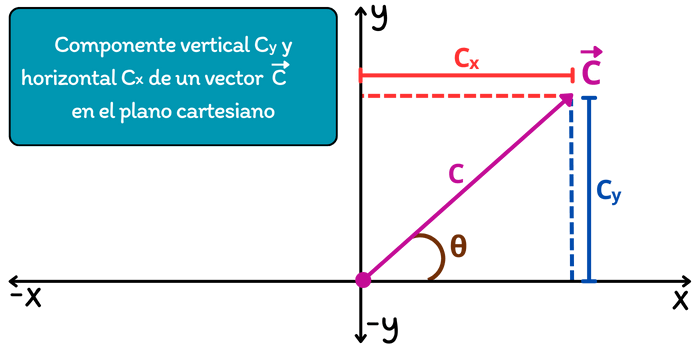
Para calcular la componente en \(y\) utilizamos la siguiente relación trigonométrica: \[\sin{\theta}=\frac{C_y}{C}\] Despejando \(C_y\) de esta igualdad, obtenemos la componente en \(y\) del vector \(\vec{C}\): \[C_y=C\sin{\theta}\] De manera similar, para determinar la componente en \(x\) utilizamos la siguiente relación trigonométrica: \[\cos{\theta}=\frac{C_x}{C}\] Al despejar \(C_x\), obtenemos la componente en \(x\) del vector \(\vec{C}\): \[C_x=C\cos{\theta}\] De esta manera, podemos expresar las componentes rectangulares del vector \(\vec{C}\) como: \[\begin{aligned}\vec{C}&=(C_x, C_y)\\&=(C\cos{\theta}, C\sin{\theta})\end{aligned}\]
Ahora, si \(\vec{C}\) es el vector resultante que se obtiene al sumar el vector \(\vec{A}\) con el vector \(\vec{B}\), entonces: \[\begin{aligned}\vec{C}&=\vec{A}+\vec{B}\\&=(A_x, A_y)+(B_x, B_y)\\&=(A_x+B_x, A_y+B_y)\end{aligned}\]
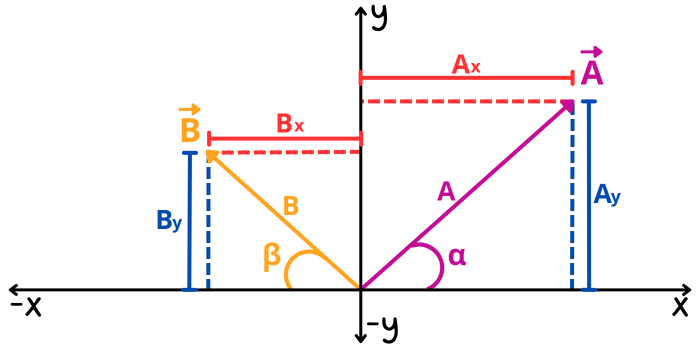
Para calcular las componentes rectangulares de los vectores \(\vec{A}\) y \(\vec{B}\), utilizamos el método anterior. Para el vector \(\vec{A}\) obtenemos: \[\begin{aligned}A_y&=A\sin{\alpha}\\A_x&=A\cos{\alpha}\end{aligned}\] Para el vector \(\vec{B}\) obtenemos: \[\begin{aligned}B_y&=B\sin{(180°-\beta)}\\B_x&=B\cos{(180°-\beta)}\end{aligned}\] Es importante tener en cuenta que los ángulos se miden siempre con respecto al eje \(x\) positivo. Un ángulo se considera positivo si se mide en sentido contrario al giro de las manecillas del reloj y negativo en caso contrario. Si bien un vector puede orientarse en cualquier dirección con respecto a cualquier eje de coordenadas, para calcular con precisión sus componentes rectangulares, es esencial tomar en cuenta el ángulo en relación con el eje \(x\) positivo, esto debido a que la dirección de un vector es el ángulo que forma con respecto al eje \(x\) positivo. Esto explica por qué aquí fue necesario considerar el ángulo del vector \(\vec{B}\) como \((180°-\beta)\).
Con esta información, podemos calcular la suma de las componentes en \(x\) de la siguiente manera: \[\begin{aligned}\sum C_x&=A_x+B_x\\&=A\cos{\alpha}+B\cos{(180°-\beta)}\end{aligned}\] Y para la suma de las componentes en \(y\): \[\begin{aligned}\sum C_y&=A_y+B_y\\&= A\sin{\alpha}+B\sin{(180°-\beta)}\end{aligned}\] Ahora que tenemos las componentes rectangulares del vector resultante \(\vec{C}\), podemos determinar su magnitud utilizando la siguiente fórmula: \[|\vec{C}|=\sqrt{(C_{x})^2+(C_y)^2}\] Y para hallar la dirección, usamos la fórmula: \[\theta=\tan^{-1}\left(\frac{C_y}{C_x}\right)\] Este método es especialmente útil cuando se trabajan con sistemas de coordenadas cartesianas y se conocen las magnitudes y direcciones de los vectores involucrados. El método analítico permite calcular la resultante de manera precisa y eficiente sin necesidad de usar métodos gráficos o geométricos, como el método del triángulo o el método del paralelogramo.
Artículo recomendado: Cantidades escalares y vectoriales