Los triángulos
Los triángulos son figuras geométricas fundamentales en la geometría, son mucho más que simplemente tres líneas conectadas en sus extremos. Estos polígonos de tres lados pueden ser clasificados de varias maneras según sus propiedades únicas, lo que nos brinda una comprensión más profunda de sus características y relaciones internas. Al analizar los diferentes tipos de triángulos, tanto en función de sus lados como de sus ángulos, revelamos una riqueza de información sobre sus simetrías, medidas y aplicaciones en diversas áreas de las matemáticas.
¿Qué es un triángulo?
Un triángulo es una figura geométrica plana compuesta por tres segmentos de línea recta que se interconectan para formar tres vértices y tres lados. Los lados son los segmentos de línea que conectan los vértices, y los vértices son los puntos donde se encuentran los lados. La suma de los ángulos internos de un triángulo es igual a 180 grados, y la longitud de la suma de dos lados de un triángulo siempre es mayor que la longitud del tercer lado, lo que se conoce como la desigualdad triangular. Los triángulos se pueden clasificar de diversas formas según sus lados y ángulos, como lo veremos a continuación. Estas clasificaciones permiten comprender mejor las propiedades y relaciones entre los diferentes tipos de triángulos.

Partes de un triángulo
Vértices: Son los puntos donde se encuentran los lados del triángulo. Un triángulo tiene siempre tres vértices. Lados: Son los segmentos de línea que conectan los vértices del triángulo. Un triángulo tiene tres lados. Ángulos: Son las aberturas formadas por los lados del triángulo en sus vértices. Un triángulo tiene tres ángulos interiores. Altura: Es la línea perpendicular trazada desde un vértice de un triángulo hasta el lado opuesto o su prolongación. Cada triángulo tiene tres alturas, una desde cada vértice. Mediana: Es una línea trazada desde un vértice hasta el punto medio del lado opuesto. Cada triángulo tiene tres medianas, una desde cada vértice. Bisectriz: Es una línea que divide un ángulo en dos partes iguales. Cada triángulo tiene tres bisectrices, una para cada ángulo. Circuncentro: Es el punto donde se cruzan las tres perpendicular bisectrices de los lados del triángulo. Se encuentra en el centro de la circunferencia circunscrita al triángulo. Incentro: Es el punto donde se cruzan las tres bisectrices interiores de los ángulos del triángulo. Se encuentra en el centro del círculo inscrito en el triángulo. Baricentro: Es el punto donde se cruzan las tres medianas del triángulo. También se llama centro de gravedad del triángulo. Ortocentro: Es el punto donde se cruzan las tres alturas del triángulo. Generalmente los lados de un triángulo se les representa por las letras \(a\), \(b\) y \(c\), mientras que los vértices se les representa por las mismas letras, pero en mayúscula, es decir, \(A\), \(B\) y \(C\). Los ángulos se les representa por las letras griegas \(\alpha\), \(\beta\) y \(\gamma\).

Tipos de triángulos
Los triángulos se clasifican de acuerdo a sus características principales: Según sus lados y según sus ángulos. Existen tres tipos de triángulos según sus lados, estos son: Triángulo equilátero, triángulo isósceles y triángulo escaleno. Además, existen tres tipos de triángulos según sus ángulos, estos son: Triángulo rectángulo, triángulo acutángulo y triángulo obtusángulo.
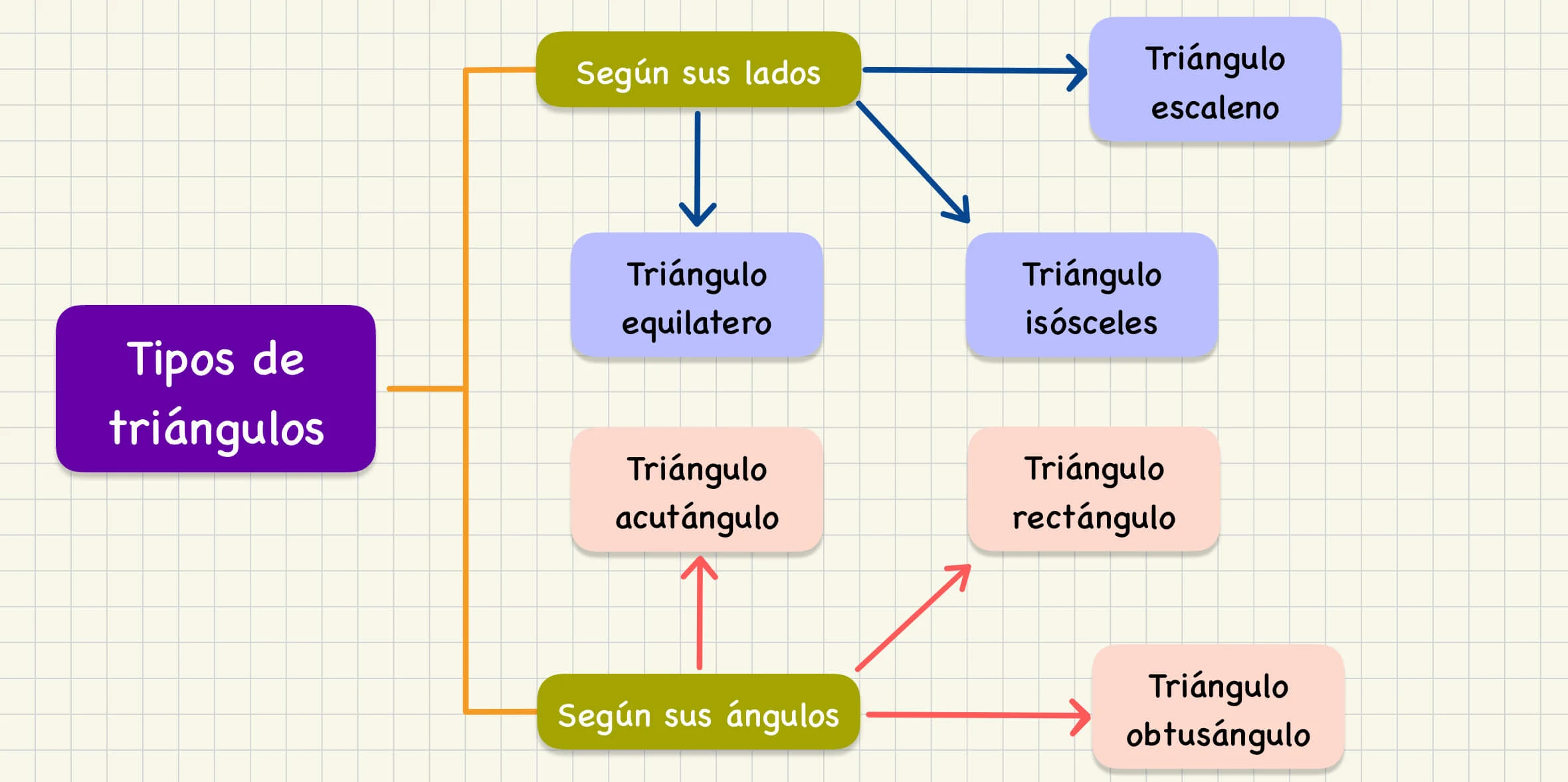
Tipos de triángulos según sus lados
Los nombres de los triángulos según sus lados son: equilátero, isósceles y escaleno. Cada uno de ellos tiene diferentes características que desarrollaremos a continuación.
Triángulo equilátero
Triángulo Equilátero: Tiene sus tres lados iguales, es decir, los tres lados son de la misma longitud. Además, todos los ángulos son iguales y miden 60 grados. El triángulo equilátero es un polígono regular.

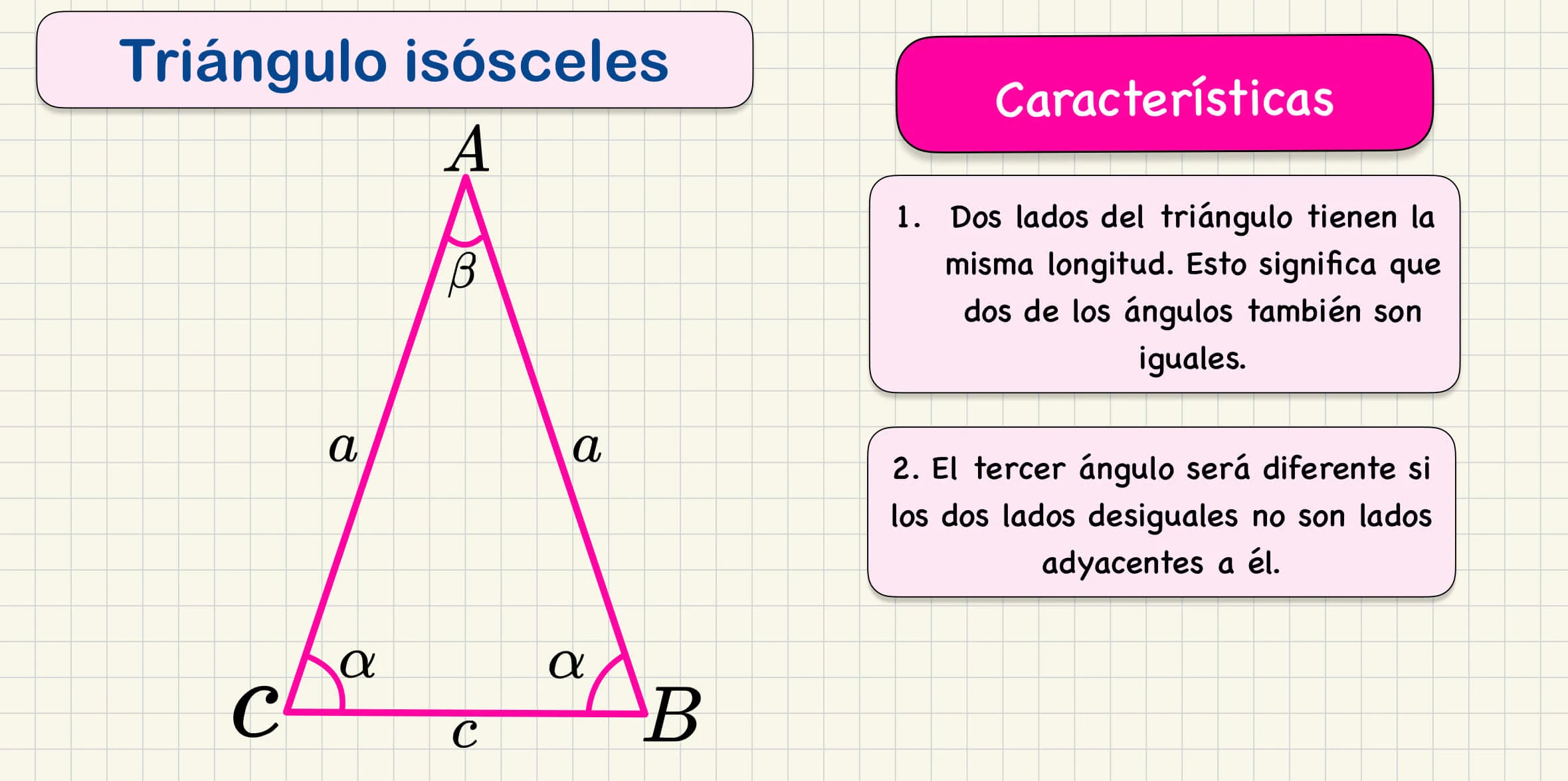
Triángulo Isósceles
Triángulo Isósceles: En un triángulo isósceles, al menos dos de los tres lados tienen la misma longitud. Esto significa que dos de los ángulos también son iguales. El tercer ángulo será diferente si los lados desiguales no son los lados adyacentes a él.
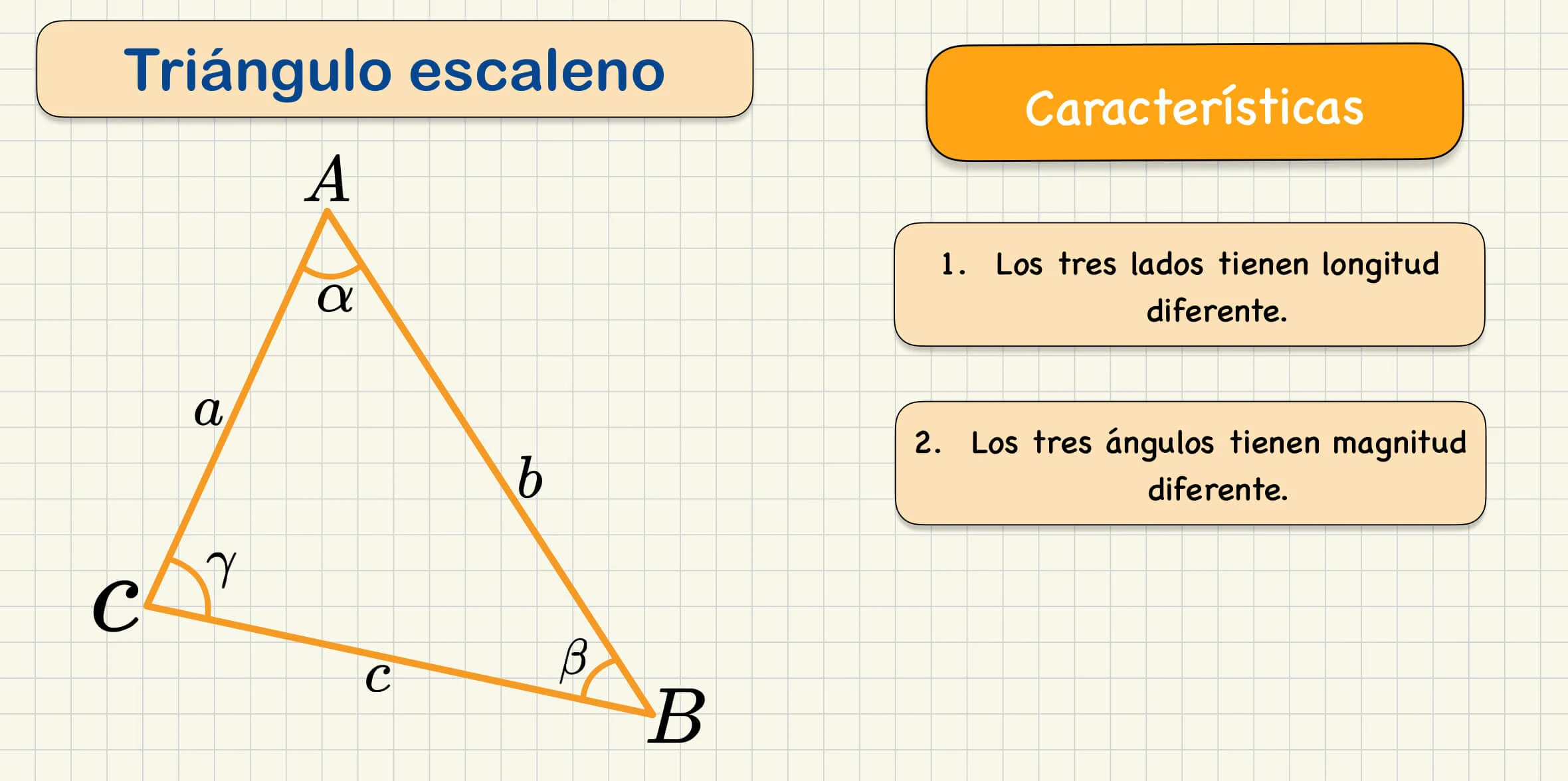
Triángulo escaleno
Triángulo Escaleno: En un triángulo escaleno, los tres lados tienen longitudes diferentes, lo que implica que todos los ángulos también son diferentes.
Tipos de triángulos según sus ángulos
Los triángulos se pueden clasificar de acuerdo a la amplitud de sus ángulos, los cuales pueden ser rectos (iguales que 90º); agudos (menores que 90º) y obtusos (mayores que 90º).
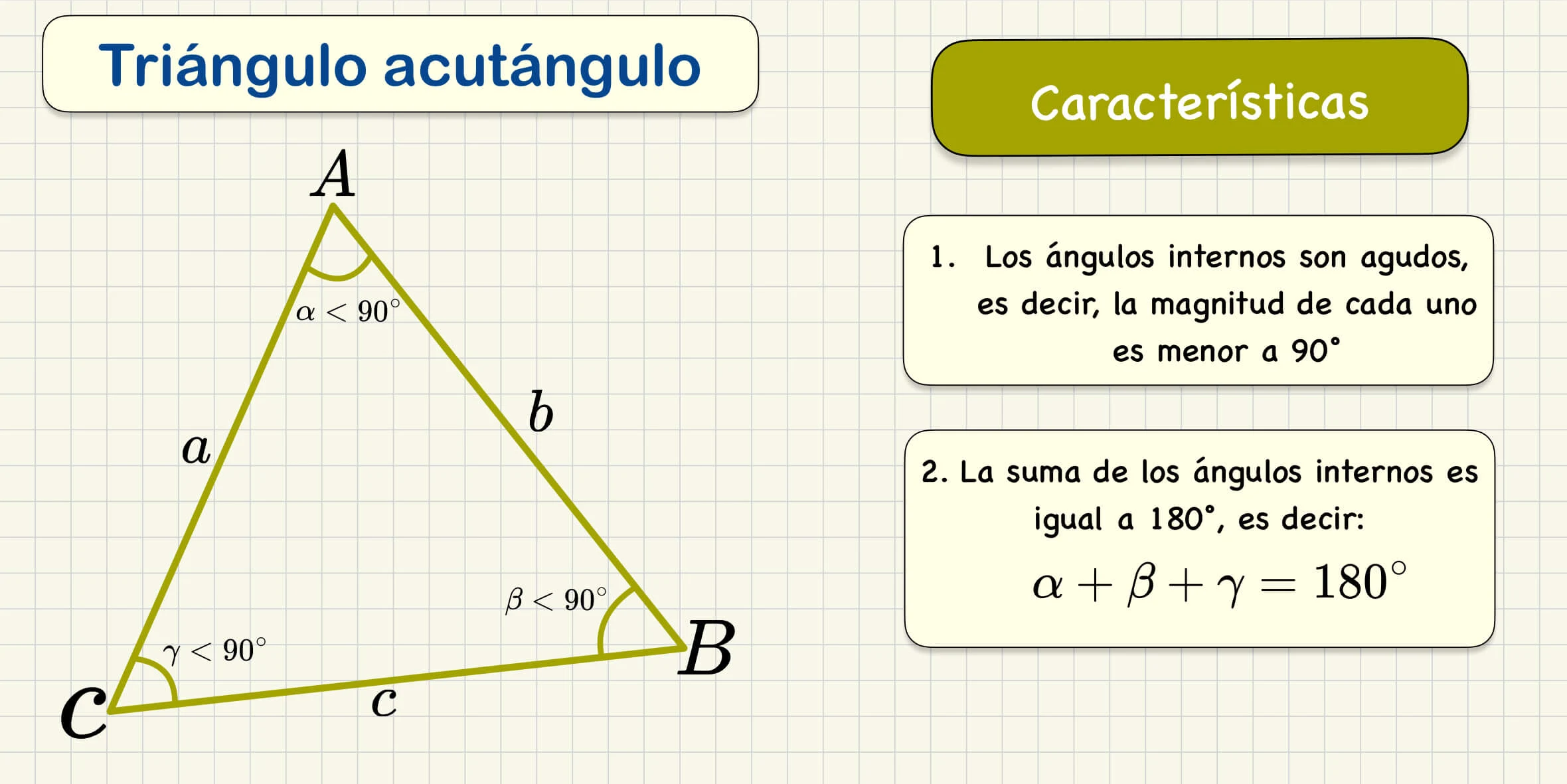
Triángulo acutángulo
Triángulo Acutángulo: En este tipo de triángulo, todos los ángulos son agudos, es decir, miden menos de 90 grados.
Triángulo rectángulo
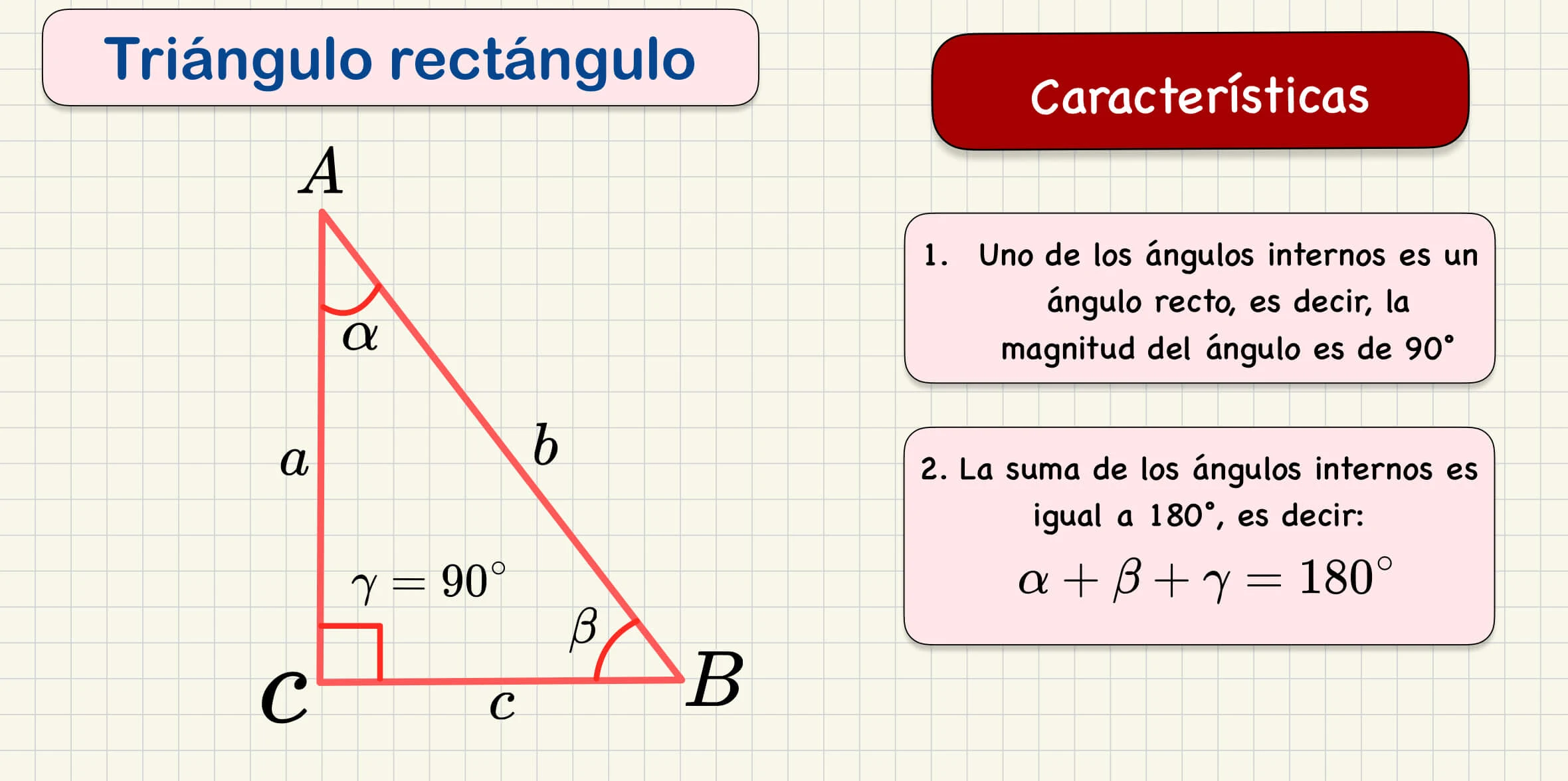
Triángulo Rectángulo: Este tipo de triángulo tiene un ángulo recto, que mide exactamente 90 grados. Los otros dos ángulos son agudos.
Triángulo obtusángulo
Triángulo Obtusángulo: En un triángulo obtusángulo, uno de los ángulos es obtuso, es decir, mide más de 90 grados.

Propiedades de los triángulos
Los triángulos son los polígonos más elementales, pero también los más singulares. Sus tres ángulos internos siempre suman 180°. Cualquier polígono puede subdividirse en triángulos de diversas maneras, siendo la más sencilla trazar sus diagonales. Curiosamente, los triángulos son únicos entre los polígonos al carecer de diagonales.
Además, todos los triángulos son tanto cíclicos (inscritos) como tangenciales (circunscritos), una característica que ningún otro tipo de polígono comparte. Determinar la medida de un ángulo o un lado desconocido en un triángulo es relativamente simple, e incluso se pueden calcular dos de sus lados o ángulos con la información adecuada.
Dado que cualquier polígono puede dividirse en triángulos, y los triángulos tienen numerosas relaciones matemáticas que son estudiadas en trigonometría, podemos aplicar las propiedades de los triángulos al estudio de otros polígonos. Esto explica por qué los triángulos son tan especiales, significativos y asombrosos.
Triángulos en la vida cotidiana
Los triángulos son una forma geométrica fundamental que se encuentra en numerosos aspectos de la vida cotidiana. Aquí hay algunas situaciones comunes en las que los triángulos desempeñan un papel importante:
Construcción y arquitectura: Los triángulos son fundamentales en la construcción y arquitectura. Los arquitectos y los ingenieros utilizan triángulos para diseñar estructuras estables, como puentes y edificios. Las vigas y las estructuras de soporte a menudo forman triángulos para distribuir la carga de manera eficiente. Navegación: Los triángulos se utilizan en navegación marítima y aérea. La trigonometría es fundamental para determinar la posición y la dirección en el mar o en el aire. Los navegantes utilizan triángulos para resolver problemas relacionados con la posición y la ruta. Diseño gráfico y arte: En el diseño gráfico y el arte, los triángulos se utilizan para crear equilibrio y armonía en composiciones visuales. Se pueden utilizar para guiar la mirada del espectador y enfocar la atención en un punto específico. Electrónica y tecnología: Los circuitos electrónicos a menudo contienen componentes en forma de triángulos, como transistores y diodos. Además, las antenas, como las antenas de teléfonos móviles, a menudo se diseñan en forma de triángulo para optimizar la recepción de señales. Música: En la música, los triángulos también desempeñan un papel. Un triángulo es un instrumento musical de percusión que se toca golpeando un metal en forma de triángulo con una barra de metal.
Estos son solo algunos ejemplos de cómo los triángulos son una parte integral de nuestra vida cotidiana en diversos campos, desde la matemática y la ciencia hasta el arte, la tecnología y la arquitectura.