Logaritmos y sus propiedades: Ejemplos

Definición de logaritmo

Un logaritmo es una función matemática que mide el exponente al cual se debe elevar un número, llamado base, para obtener otro número específico. En otras palabras, el logaritmo de un número \(x\) en una base \(a\), denotado como \(\log_a(x)\), es el exponente \(y\) al cual se debe elevar \(a\) para obtener \(x\).

La notación correspondiente para representar a un logaritmo es la siguiente: \[\log_a(x)=y\Leftrightarrow a^{y}=x\]

¿Qué son las propiedades los logaritmos?

Las propiedades de los logaritmos son reglas matemáticas que describen su comportamiento en diversas operaciones. Estas reglas son esenciales para simplificar expresiones logarítmicas, resolver ecuaciones y realizar cálculos de manera exacta.

¿Cuáles son las propiedades los logaritmos?

Las principales propiedades de los logaritmos incluyen la propiedad del logaritmo de un producto, la propiedad del logaritmo de un cociente, la propiedad del logaritmo de una potencia, la propiedad del logaritmo del recíproco, la propiedad del logaritmo de una raíz y la propiedad del cambio de base de un logaritmo. Las propiedades secundarias de los logaritmos se derivan de la definición de logaritmo. Estas incluyen la propiedad del logaritmo de uno, la propiedad del logaritmo de la base, la propiedad del logaritmo de un número negativo, la propiedad del logaritmo de cero y la propiedad del logaritmo de base negativa. A continuación, se presentan las propiedades de los logaritmos y lo que establece cada una.

Logaritmo de un producto

Propiedad del logaritmo de un producto: Si \(x, y >0\), entonces se cumple que: \[\log_{a}(x\cdot y)=\log_{a}(x)+\log_{a}(y)\] Esta propiedad establece que el logaritmo base \(a\) de un producto es igual a la suma de los logaritmos base \(a\) de los factores.

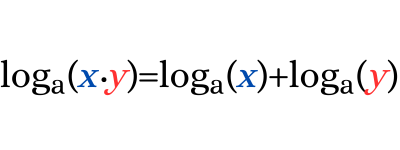
Logaritmo de un producto ejemplos

Ejemplo 1. \[\begin{aligned}\log_2(8)&=\log_2(2\cdot 4)\\&=\log_2(2)+\log_2(4)\\&=1+2\\&=3\end{aligned}\] Ejemplo 2. \[\begin{aligned}\log_2(32)&=\log_2(4\cdot 8)\\&=\log_2(4)+\log_2(8)\\&=2+3\\&=5\end{aligned}\]

Logaritmo de un cociente

Propiedad del logaritmo de un cociente: Si \(x, y >0\), entonces se cumple que: \[\log_{a}\left(\frac{x}{y}\right)=\log_{a}(x)-\log_{a}(y)\] Esta propiedad establece que el logaritmo base \(a\) de un cociente es igual al logaritmo base \(a\) del dividendo menos el logaritmo base \(a\) del divisor.

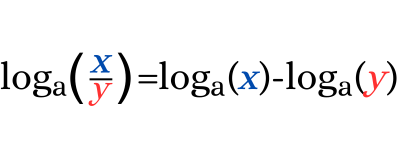
Logaritmo de un cociente ejemplos

Ejemplo 3. \[\begin{aligned}\log_5\left(\frac{25}{5}\right)&=\log_5(25)-\log_5(5)\\&=2-1\\&=1\end{aligned}\] Ejemplo 4. \[\begin{aligned}\log_2\left(\frac{8}{4}\right)&=\log_2(8)-\log_2(4)\\&=3-2\\&=1\end{aligned}\] Ejemplo 5. \[\begin{aligned}\log_3(45)-\log_3(5)&=\log_3\left(\frac{45}{5}\right)\\&=\log_3(9)\end{aligned}\]

Logaritmo de una potencia

Propiedad del logaritmo de una potencia. Para \(x>0\) y \(n\) un número natural, se cumple que: \[\log_{a}(x^n)=n\cdot\log_{a}(x)\] Esta propiedad establece que el logaritmo base \(a\) de una potencia es igual al producto del exponente por el logaritmo base \(a\) de la base de la potencia.

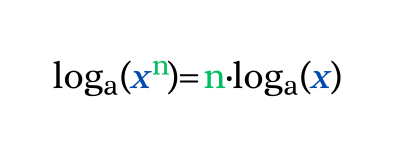
Logaritmo de una potencia ejemplos

Ejemplo 6. \[\begin{aligned}\log_3(27^2)&=2\cdot\log_3(27)\\&=2\cdot 3\\&=6\end{aligned}\] Ejemplo 7. \[\begin{aligned}\log_2(8^4)&=4\cdot\log_2(8)\\&=4\cdot 3\\&=12\end{aligned}\]

Logaritmo del recíproco

Propiedad del logaritmo del recíproco. Si \(x>0\), entonces se cumple que: \[\log_a{\frac{1}{x}}=-\log_a{x}\] Esta propiedad establece que el logaritmo base \(a\) del recíproco de \(x\) es el opuesto del logaritmo base \(a\) de \(x\).

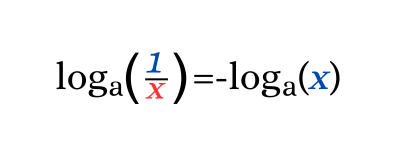
Logaritmo del reciproco ejemplos

Ejemplo 8. \[\ln{\frac{1}{5}}=-\ln{5}\] Ejemplo 9. \[\ln{\frac{1}{10}}=-\ln{10}\] Ejemplo 10. \[-\ln{3}=\ln{\left(\frac{1}{3}\right)}\]

Logaritmo de una raíz

Propiedad del logaritmo de una raíz: \[\log_{a}(\sqrt[n]{x})=\frac{1}{n}\log_{a}(x)\] Esta propiedad establece que el logaritmo base \(a\) de una raíz es igual al cociente entre el logaritmo base \(a\) del radicando y el índice de la raíz.

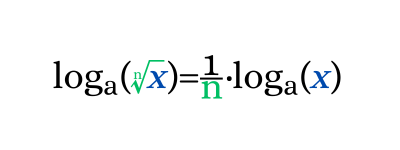
Logaritmo de una raíz ejemplos

Ejemplo 11. \[\begin{aligned}\log_4(\sqrt[6]{16})&=\frac{1}{6}\cdot\log_4(16)\\&=\frac{1}{6}\cdot\log_4(4^2)\\&=\frac{1}{6}\cdot 2\cdot\log_4(4)\\&=\frac{1}{6}\cdot 2\cdot 1\\&=\frac{2}{6}\\&=\frac{1}{3}\end{aligned}\] Ejemplo 12. \[\begin{aligned}\log_2(\sqrt[4]{8})&=\frac{1}{4}\cdot\log_2(8)\\&=\frac{1}{4}\cdot 3\\&=\frac{3}{4}\end{aligned}\] Ejemplo 13. \[\begin{aligned}8\log_5(\sqrt{5})&=8\frac{1}{2}\log_5(5)\\&=4\log_5(5)\end{aligned}\]

Cambio de base de un logaritmo

Propiedad del cambio de base de un logaritmo: \[\log_{a}(x)=\frac{\log_{b}(x)}{\log_{b}(a)}\] Esta propiedad establece que puedes cambiar la base de un logaritmo dividiendo su logaritmo en otra base entre el logaritmo de esa misma base.

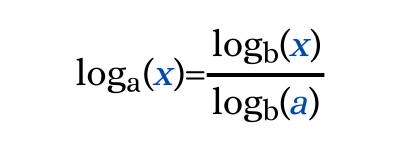
Cambio de base de un logaritmo ejemplos

Ejemplo 14. \[\begin{aligned}\log_2(4)&=\frac{\log_4(4)}{\log_4(2)}\\&=\frac{1}{\frac{1}{2}}\\&=2\end{aligned}\] Ejemplo 15. \[\begin{aligned}\log_2(16)&=\frac{\log_{10}(16)}{\log_{10}(2)}\\&=\frac{1.2041}{0.3010}\\&=\approx 4\end{aligned}\]

Es importante destacar que, para aplicar las propiedades de los logaritmos, las bases de los logaritmos tienen que ser iguales. Por ejemplo, una suma de logaritmos se puede escribir como el logaritmo de un producto, pero solo si la base de los logaritmos de los sumandos es la misma.

A continuación, veamos las propiedades secundarias de los logaritmos, las cuales se derivan a partir de la definición de logaritmo.

Logaritmo de uno

Propiedad del logaritmo de 1: Si \(x=1\), entonces \(\log_a(1)=0\). Esta propiedad establece que el logaritmo base \(a\) de uno es igual a cero. Esto debido a que cualquier número diferente de cero elevado al exponente cero es igual a uno.

Logaritmo de la base

Propiedad del logaritmo de la base: Si \(x=a\), entonces \(\log_a(a)=1\) Esta propiedad establece que el logaritmo base \(a\) de \(a\) es igual a uno. Esto debido a que para cualquier valor de \(a\) se cumple que \(a\) elevado al exponente uno es igual a \(a\).

Logaritmo de un número negativo

Propiedad del logaritmo de un número negativo: Si \(x<0\), entonces \(\log_a{x}\) está indefinido. Esta propiedad establece que el logaritmo natural de cualquier número negativo no está definido, es decir, no existe.

Logaritmo de cero

Propiedad del logaritmo de cero: Si \(x=0\), entonces \(\log_a{0}\) está indefinido. Esta propiedad establece que el logaritmo base \(a\) de cero está indefinido, es decir, no existe.

Logaritmo de base negativa

Propiedad del logaritmo de base negativa: Si \(a<0\), entonces \(\log_a{x}\) está indefinido. Esta propiedad establece que no existe el logaritmo con base negativa.

Propiedades de los logaritmos ejercicios para practicar

Ejercicio 1. Calcular el valor del siguiente logaritmo: \[\log_4(64)\]

Ejercicio 2. Obtener el valor del siguiente logaritmo: \[\log_5(125)\]

Ejercicio 3. Hallar el valor del siguiente logaritmo: \[\log_3\left(\frac{1}{27}\right)\]

Ejemplo 4. Aplicando las propiedades de los logaritmos, simplifica la siguiente expresión: \[\log_2(8)+\log_2(32)\]

Ejercicio 5. Aplica las propiedades de los logaritmos para simplificar la siguiente expresión: \[\log_7(49)-\log_7(7)\]

Ejercicio 6. Calcular el valor del siguiente logaritmo: \[\log_9(81^{\frac{3}{2}})\]

Ejercicio 7. Aplica las propiedades de los logaritmos para determinar el valor de la siguiente expresión: \[\log_6(36)-\log_6(6)\]

Ejercicio 8. Simplifica la siguiente expresión logarítmica: \[\log_4(2)+\log_4(8)\]

Ejercicio 9. Determinar el valor de la siguiente expresión con logaritmos: \[\frac{\log_{2}(16)}{\log_{2}(4)}\]