Tabla de fórmulas de las derivadas para descargar

Fórmulas de derivadas

Las fórmulas de las derivadas son reglas matemáticas que se utilizan para calcular la derivada de una función.

La derivada de una función \(f\) se denota comúnmente por \(f'(x)\) o \(\frac{df}{dx}\) y se puede calcular aplicando diversas reglas y fórmulas. Algunas de las fórmulas básicas incluyen la derivada de una constante, la derivada de una potencia de \(x\), la derivada de funciones trigonométricas, la derivada de funciones exponenciales y logarítmicas, así como la derivada de funciones algebraicas que abarcan las reglas de suma, resta, producto y cociente.

A continuación, presentamos una tabla con las fórmulas de las derivadas inmediatas de funciones fundamentales en cálculo diferencial. También se incluye un ejemplo resuelto para cada tipo de derivada, lo que te ayudará a comprender el proceso de derivación.

Tabla de fórmulas de derivadas inmediatas

Una tabla de fórmulas de derivadas inmediatas se convierte en una herramienta valiosa al estudiar cálculo diferencial, ya que presenta manera rápida y conveniente las derivadas de las funciones más comunes.

Puedes utilizar esta tabla como referencia rápida para calcular derivadas en diversos problemas de cálculo diferencial. Recuerda que estas fórmulas son fundamentales y sirven como punto de partida para derivadas más complejas, como aquellas en las que se tenga una función compuesta y sea necesario aplicar la regla de la cadena.

Puedes descargar la tabla completa con las fórmulas de derivadas inmediatas en formato PDF para imprimir de manera gratuita haciendo clic en el botón que aparece a continuación.

Descargar fórmulas de derivadas inmediatas en PDF

Tabla de fórmulas de la derivada de una función compuesta

En el apartado anterior, hemos explorado la tabla que contiene las fórmulas de las derivadas de funciones fundamentales. Ahora surge la pregunta: ¿cómo derivar una función compuesta? En la siguiente tabla, se presentan todas las fórmulas para hallar la derivada de una función compuesta.

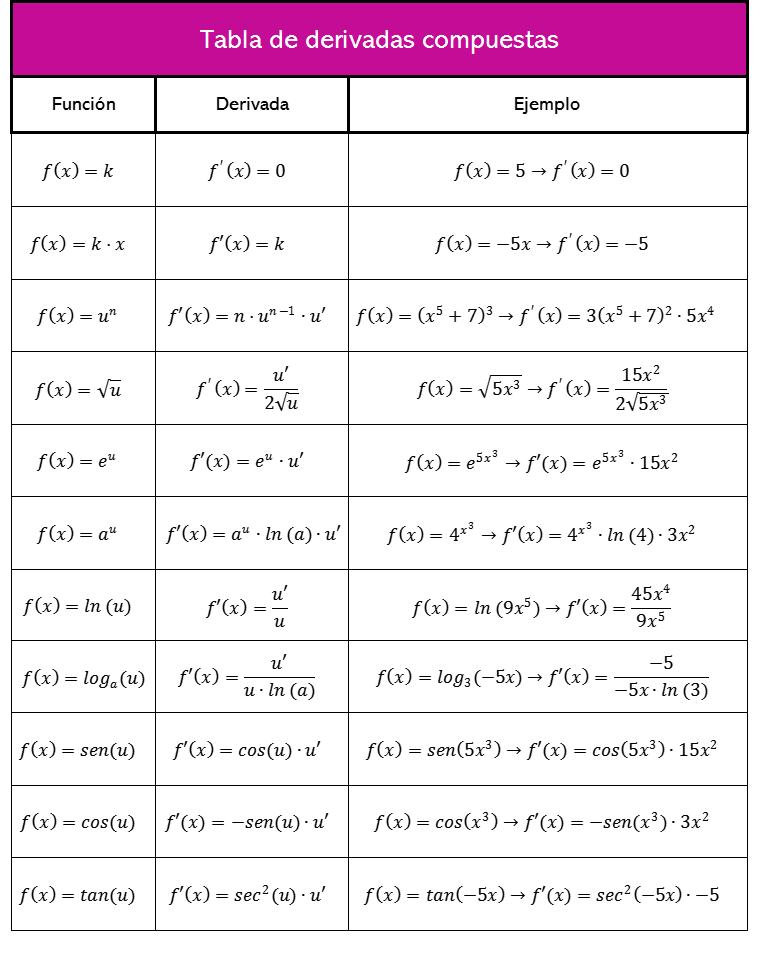
Las derivadas compuestas siguen las mismas reglas que las derivadas inmediatas, pero con la aplicación crucial de la regla de la cadena.

Te invitamos a descargar de manera gratuita la tabla completa con las fórmulas de derivadas de funciones compuestas en formato PDF, listas para imprimir. Haz clic en el botón a continuación para acceder a este recurso que facilitará tu estudio y comprensión de la derivada de una función compuesta.

Descargar tabla de derivadas de funciones compuestas en PDF

Fórmulas de la derivada de funciones algebraicas

Las funciones algebraicas son aquellas que se construyen mediante operaciones algebraicas básicas, tales como la suma, la resta, la multiplicación y la división, así como también la combinación de estas operaciones. Al derivar funciones algebraicas, se aplican reglas específicas, a continuación, te presentamos las fórmulas fundamentales para calcular la derivada de una función algebraica.

Fórmula de la derivada de una constante

Si \(f(x)=k\), entonces: \[f’(x)=0\]

Fórmula de la derivada de una constante por una función

Si \(f(x)=k\cdot g(x)\), entonces: \[f’(x)=k\cdot g’(x)\]

Fórmula de la derivada de x

Si \(f(x)=x\), entonces: \[f’(x)=1\]

Fórmula de la derivada de una potencia

Si \(f(x)=x^n\), entonces: \[f’(x)=n\cdot x^{n-1}\]

Fórmula de la derivada de una raíz

Si \(f(x)=\sqrt[n]{x}\), donde \(n\) es un número constante y \(n \neq 0\), entonces: \[f’(x)=\frac{1}{n}\cdot x^{\frac{1}{n}-1}\]

Fórmula de la derivada de una suma

Si \(f(x)=g(x)+h(x)\), entonces: \[f’(x)=g’(x)+h’(x)\]

Fórmula de la derivada de una resta

Si \(f(x)=g(x)-h(x)\), entonces: \[f’(x)=g’(x)-h’(x)\]

Fórmula de la derivada de un producto

Si \(f(x)=g(x)\cdot h(x)\), entonces: \[f’(x)=g’(x)\cdot h(x)+g(x)\cdot h’(x)\]

Fórmula de la derivada de una división

Si \(f(x)=g(x)/h(x)\) y \(h(x)\neq 0\), entonces: \[f’(x)=\frac{g’(x)\cdot h(x)-g(x)\cdot h’(x)}{\left(h(x)\right)^2}\]

Tabla de fórmulas del álgebra de derivadas

Ahora, en este apartado, presentamos una tabla completa que abarca las operaciones básicas con funciones.

Descarga nuestra tabla de fórmulas de derivadas de funciones algebraicas en formato PDF para acceder de manera rápida y fácil a las reglas básicas de la derivación.

Descargar tabla del álgebra de derivadas en PDF

Fórmulas de la derivada de las funciones exponenciales y logarítmicas

Las funciones exponenciales y logarítmicas son fundamentales en matemáticas y ciencias aplicadas. A continuación, te presentamos las fórmulas de derivadas para estas funciones:

Fórmulas de la derivada de la función exponencial

Derivada de \(e^x\). Si \(f(x)=e^x\), entonces: \[f’(x)=e^x\]

Derivada de \(a^x\) (donde \(a\) es una constante positiva). Si \(f(x)=a^x\), entonces: \[f’(x)=a^x\cdot\ln(a)\]

Fórmulas de la derivada de la función logaritmo

Derivada del logaritmo natural \(\ln(x)\). Si \(f(x)=\ln{|x|}\), entonces: \[f’(x)=\frac{1}{x}\]

Derivada del logaritmo base \(a\) de \(x\); \(\log_a(x)\) (donde \(a\) es una constante positiva y \(a\neq 1\)). Si \(f(x)=\log_a(x)\), entonces: \[f’(x)=\frac{1}{x\cdot\ln(a)}\]

Tabla de fórmulas de la derivada de las funciones exponenciales y logarítmicas

A continuación, te presentamos una tabla con las fórmulas de las derivadas de las funciones exponenciales y logarítmicas.

Descarga la tabla de fórmulas de derivadas para funciones exponenciales y logarítmicas en formato PDF a continuación.

Descargar tabla de la derivada de las funciones exponenciales y logarítmicas en PDF

Fórmulas de la derivada de las funciones trigonométricas

Las funciones trigonométricas son funciones matemáticas que involucran las razones entre los lados de un triángulo rectángulo y se utilizan ampliamente en diversas áreas de las matemáticas y las ciencias. A continuación, presentamos las fórmulas de derivadas de las funciones trigonométricas fundamentales.

Derivada del seno

Si \(f(x)=\sin(x)\), entonces: \[f’(x)=\cos{x}\]

Derivada del coseno

Si \(f(x)=\cos(x)\), entonces: \[f’(x)=-\sin{x}\]

Derivada de la tangente

Si \(f(x)=\tan(x)\), entonces: \[f’(x)=\sec^2{x}\]

Derivada de la cosecante

Si \(f(x)=\csc(x)\), entonces: \[f’(x)=-\csc(x)\cdot\cot(x)\]

Derivada de la secante

Si \(f(x)=\sec(x)\), entonces: \[f’(x)=\sec(x)\cdot\tan(x)\]

Derivada de la cotangente

Si \(f(x)=\cot(x)\), entonces \[f’(x)=-\csc^2(x)\]

Tabla de fórmulas de la derivada de las funciones trigonométricas

La siguiente tabla agrupa las fórmulas de las derivadas de las funciones trigonométricas fundamentales.

A continuación, puedes descargar esta tabla en formato PDF de manera gratuita para que puedas llevarla contigo y utilizarla cuando lo requieras.

Descargar tabla de la derivada de las funciones trigonométricas en PDF

Fórmulas de la derivada de las funciones trigonométricas inversas

Las funciones trigonométricas inversas son las inversas de las funciones trigonométricas fundamentales y se denotan comúnmente por \(\arcsin(x)\), \(\arccos(x)\), \(\arctan(x)\), \(\text{arccsc}(x)\), \(\text{arcsec}(x)\) y \(\text{arccot}(x)\). A continuación, te presentamos las fórmulas de las derivadas de las funciones trigonométricas inversas:

Derivada del arcoseno

Si \(f(x)=\arcsin(x)\), entonces: \[f’(x)=\frac{1}{\sqrt{1-x^2}}\]

Derivada del arcocoseno

Si \(f(x)=\arccos(x)\), entonces: \[f’(x)=-\frac{1}{\sqrt{1-x^2}}\]

Derivada del arcotangente

Si \(f(x)=\arctan(x)\), entonces: \[f’(x)=\frac{1}{1+x^2}\]

Derivada del arcocosecante

Si \(f(x)=\text{arccsc}(x)\), entonces: \[f’(x)=-\frac{1}{x\cdot\sqrt{x^2-1}}\]

Derivada del arcosecante

Si \(f(x)=\text{arcsec}(x)\), entonces: \[f’(x)=\frac{1}{x\cdot\sqrt{x^2-1}}\]

Derivada del arcocotangente

Si \(f(x)=\text{arccot}(x)\), entonces: \[f’(x)=-\frac{1}{1+x^2}\]

Tabla de fórmulas de la derivada de las funciones trigonométricas inversas

En la siguiente imagen, se presenta una tabla detallada con las fórmulas de las derivadas de las funciones trigonométricas inversas.

Puedes descargar de forma gratuita la tabla de derivadas trigonométricas inversas en formato PDF. Esta herramienta esencial ofrece una referencia rápida y práctica para calcular las derivadas de las funciones trigonométricas inversas.

Descargar tabla de la derivada de las funciones trigonométricas inversas en PDF

Fórmulas de la derivada de las funciones hiperbólicas

Las funciones hiperbólicas son análogas a las funciones trigonométricas, pero se definen en términos de las funciones exponenciales. Las funciones hiperbólicas son \(\sinh(x)\) (seno hiperbólico), \(\cosh(x)\) (coseno hiperbólico), \(\tanh(x)\) (tangente hiperbólica), \(\coth(x)\) (cotangente hiperbólica), \(\text{sech}(x)\) (secante hiperbólica), y \(\text{csch}(x)\) (cosecante hiperbólica). A continuación, te presentamos las fórmulas de las derivadas de las funciones hiperbólicas fundamentales.

Derivada del seno hiperbólico

Si \(f(x)=\sinh(x)\), entonces: \[f’(x)=\cosh(x)\]

Derivada del coseno hiperbólico

Si \(f(x)=\cosh(x)\), entonces: \[f’(x)=\sinh(x)\]

Derivada de la tangente hiperbólica

Si \(f(x)=\tanh(x)\), entonces: \[f’(x)=\text{sech}^2(x)\]

Derivada de la cosecante hiperbólica

Si \(f(x)=\text{csch}(x)\), entonces: \[f’(x)=-\text{csch}(x)\coth(x)\]

Derivada de la secante hiperbólica

Si \(f(x)=\text{sech}(x)\), entonces: \[f’(x)=-\text{sech}(x)\tanh(x)\]

Derivada de la cotangente hiperbólica

Si \(\coth(x)\), entonces: \[f’(x)=-\text{csch}^2(x)\]

Estas fórmulas son similares a las derivadas de las funciones trigonométricas, pero utilizan las funciones hiperbólicas en lugar de las trigonométricas.

Tabla de fórmulas de la derivada de las funciones hiperbólicas

Presentamos la siguiente tabla que agrupa las fórmulas de las derivadas de las funciones trigonométricas inversas.

Te invitamos a descargar esta útil tabla en formato PDF de manera totalmente gratuita. Imprímela y utilízala cuando más la necesites.

Descargar tabla de la derivada de las funciones hiperbólicas en PDF

Fórmulas de la derivada de las funciones hiperbólicas inversas

Las funciones hiperbólicas inversas son las funciones inversas de las funciones hiperbólicas fundamentales y se denotan comúnmente por \(\text{arsinh}(x)\) (seno hiperbólico inverso), \(\text{arcosh}(x)\) (coseno hiperbólico inverso), \(\text{artanh}(x)\) (tangente hiperbólica inversa), \(\text{arcoth}(x)\) (cotangente hiperbólica inversa), \(\text{arsech}(x)\) (secante hiperbólica inversa), y \(\text{arcsch}(x)\) (cosecante hiperbólica inversa). A continuación, te presentamos las fórmulas de derivadas para estas funciones:

Derivada del arcoseno hiperbólico

Si \(f(x)=\text{arsinh}(x)\), entonces: \[f’(x)=\frac{1}{\sqrt{x^2+1}}\]

Derivada del arcocoseno hiperbólico

Si \(f(x)=\text{arcosh}(x)\), entonces: \[f’(x)=\frac{1}{\sqrt{x^2-1}}\]

Derivada de la arcotangente hiperbólica

Si \(f(x)=\text{artanh}(x)\), entonces: \[f’(x)=\frac{1}{1-x^2}\]

Derivada del arcocosecante hiperbólico

Si \(\text{arcsch}(x)\), entonces: \[f’(x)=-\frac{1}{|x|\cdot\sqrt{x^2+1}}\]

Derivada del arcosecante hiperbólico

Si \(f(x)=\text{arsech}(x)\), entonces: \[f’(x)=-\frac{1}{x\sqrt{1-x^2}}\]

Derivada del arcocotangente hiperbólico

Si \(f(x)=\text{arcoth}(x)\), entonces: \[f’(x)=\frac{1}{1-x^2}\]

Tabla de fórmulas de la derivada de las funciones hiperbólicas inversas

A continuación, te presentamos una tabla que resume todas las derivadas de las funciones hiperbólicas inversas.

Descarga ahora la tabla completa de derivadas de las funciones hiperbólicas inversas en formato PDF. Este recurso gratuito te permitirá tener a tu disposición estas fórmulas esenciales, listas para ser utilizadas cuando más las necesites.

Descargar tabla de la derivada de las funciones hiperbólicas inversas en PDF

Tabla completa de derivadas

Explora y descarga en PDF nuestra tabla completa de derivadas que presenta todas las fórmulas y reglas de derivación. Esta tabla es un recurso integral que puedes utilizar para tus estudios, ya que resume todas las derivadas que hemos abordado anteriormente.

Descargar tabla completa de fórmulas de la derivada en PDF