Recíproco de un número real

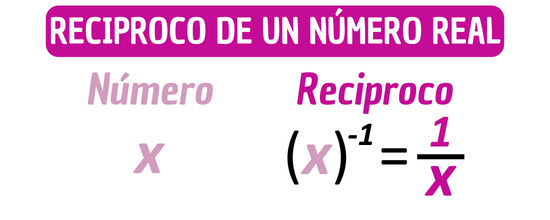
El recíproco de un número real "x", diferente de cero, es aquel número que, cuando se multiplica por "x", da como resultado 1.

El recíproco de un número real "x" diferente de cero es igual a una potencia de base "x" y exponente -1. Matemáticamente, se representa de la siguiente manera: \[x^{-1}\]

En otras palabras, el recíproco de un número real $x$ diferente de cero es el inverso multiplicativo de $x$. Por lo tanto, si $x$ es un número real diferente de cero, entonces su recíproco es $\frac{1}{x}$, ya que: \[\begin{aligned}x\cdot x^{-1}&=x\cdot\frac{1}{x}\\&=\frac{x}{x}\\&=1\end{aligned}\]

Ejemplos del recíproco de un número

Ejemplo 1. El recíproco de 3 es 1/3, ya que: \[\begin{aligned}3\cdot\frac{1}{3}&=\frac{3}{3}\\&=1\end{aligned}\]

Ejemplo 2. El recíproco de 12 es 1/12, ya que: \[\begin{aligned}12\cdot\frac{1}{12}&=\frac{12}{12}\\&=1\end{aligned}\]

Ejemplo 3. El recíproco de π es 1/π, ya que: \[\begin{aligned}π\cdot\frac{1}{π}&=\frac{π}{π}\\&=1\end{aligned}\]

¿Cómo se calcula el recíproco de un número?

Para calcular el recíproco de un número real $x$ diferente de cero, simplemente se divide 1 entre dicho número $x$. Por ejemplo, para calcular el recíproco de 7, simplemente se divide 1 entre 7, es decir, el recíproco de 7 es igual a la fracción 1/7.

De manera similar, el recíproco de 2 es igual a 1/2.

Este procedimiento para calcular el recíproco de un número es válido para cualquier número real $x$ diferente de cero, ya sea positivo, negativo, racional o irracional.

Recíproco de un número negativo

El recíproco de un número real negativo $-x$ se denota como $(-x)^{-1}$ y es igual a: \[-\frac{1}{x}\]

El recíproco de un número real negativo $-x$ se calcula dividiendo 1 entre dicho número real negativo $-x$ y aplicando la ley de los signos en la división. Por ejemplo, el recíproco de -2 es igual a $-\frac{1}{2}$ ya que: \[\begin{aligned}(-2)^{-1}&=\frac{1}{-2}\\&=\frac{+1}{-2}\\&=-\frac{1}{2}\end{aligned}\]

De manera similar, el recíproco de -7 es igual a $-\frac{1}{7}$ ya que al dividir 1 entre -7 obtenemos: \[\begin{aligned}(-7)^{-1}&=\frac{1}{-7}\\&=\frac{+1}{-7}\\&=-\frac{1}{7}\end{aligned}\]

Recíproco de un número racional

El recíproco de un número racional $\frac{a}{b}$, donde $a\neq 0$ y $b\neq 0$, se denota como $\left(\frac{a}{b}\right)^{-1}$ y es igual a: \[\frac{b}{a}\]

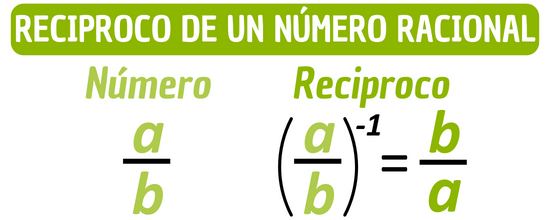
$El recíproco de una fracción es igual a la misma fracción, pero invertida, es decir, es igual a una fracción con el numerador en el lugar del denominador y viceversa$

El recíproco de un número racional se calcula dividiendo 1 entre el número racional en cuestión, o simplemente invirtiendo la fracción, es decir, pasando el numerador al lugar del denominador y viceversa. Por ejemplo, el recíproco de $\frac{2}{3}$ es igual a $\frac{3}{2}$, ya que: \[\begin{aligned}\left(\frac{2}{3}\right)^{-1}&=\frac{1}{\frac{2}{3}}\\&=\frac{\frac{1}{1}}{\frac{2}{3}}\\&=\frac{3\cdot 1}{2\cdot 1}\\&=\frac{3}{2}\end{aligned}\]

Como se puede observar, este mismo resultado se obtiene directamente al invertir la fracción, es decir: \[\left(\frac{2}{3}\right)^{-1}=\frac{3}{2}\]

De manera similar, el recíproco de $\frac{3}{-4}$ es igual a $-\frac{4}{3}$, ya que al dividir 1 entre la fracción $\frac{3}{4}$ obtenemos: \[\begin{aligned}\left(\frac{3}{-4}\right)^{-1}&=\frac{1}{\frac{3}{-4}}\\&=\frac{\frac{1}{1}}{\frac{3}{-4}}\\&=\frac{-4\cdot 1}{3\cdot 1}\\&=\frac{-4}{3}\\&=-\frac{4}{3}\end{aligned}\]

Nuevamente, se observa que este mismo resultado se obtiene directamente al invertir la fracción. Es decir, el recíproco de una fracción es igual a la misma fracción, pero invertida considerando su signo, es decir: \[\left(\frac{3}{-4}\right)^{-1}=-\frac{4}{3}\]

Recíproco de un número racional con numerador 1

El recíproco de un número racional con numerador 1, definido por $\frac{1}{x}$, donde $x\neq 0$, se denota como $\left(\frac{1}{x}\right)^{-1}$ y es igual al número entero $x$.

$El recíproco de un número racional con numerador uno, es igual al número entero que representa el denominador de la fracción$

El recíproco de un número racional con numerador 1 se calcula dividiendo 1 entre el número racional en cuestión, o simplemente invirtiendo la fracción, es decir, pasando el numerador al lugar del denominador y el denominador al lugar del numerador, y luego efectuando la división. Por ejemplo, el recíproco de $\frac{1}{5}$ se denota como $\left(\frac{1}{5}\right)^{-1}$ y es igual a 5. Este resultado se obtiene dividiendo 1 entre $\frac{1}{5}$, es decir: \[\begin{aligned}\left(\frac{1}{5}\right)^{-1}&=\frac{1}{\frac{1}{5}}\\&=\frac{\frac{1}{1}}{\frac{1}{5}}\\&=\frac{5\cdot 1}{1\cdot 1}\\&=\frac{5}{1}\\&=5\end{aligned}\]

Como se puede observar, este mismo resultado se obtiene directamente al invertir el numerador al lugar del denominador y viceversa, es decir: \[\begin{aligned}\left(\frac{1}{5}\right)^{-1}&=\frac{5}{1}\\&=5\end{aligned}\]

Aplicaciones del recíproco

Entre las principales aplicaciones del cálculo del recíproco de un número, destaca su uso para resolver ecuaciones simples y para dividir fracciones.

El recíproco de un número se utiliza en la resolución de ecuaciones simples. Esto se debe a que el recíproco de un número permite cancelar valores en una ecuación, ya que el producto de un número por su recíproco siempre es igual a 1. Por ejemplo, consideremos la ecuación $\frac{2}{3}x=8$. Si multiplicamos ambos lados por el recíproco del coeficiente de la variable $x$ ($\frac{2}{3}$), dicho coeficiente se convierte en 1. Entonces, como el recíproco de la fracción $\frac{2}{3}$ es $\frac{3}{2}$, al multiplicar ambos lados obtenemos que:

\[\begin{aligned}\frac{2}{3}x&=8\\\frac{2}{3}\cdot\left(\frac{2}{3}\right)^{-1} &=8\cdot\left(\frac{2}{3}\right)^{-1}\\\frac{2}{3}\cdot \frac{3}{2}x &=8\cdot\frac{3}{2}\\x&=\frac{24}{2}\\x&=12\end{aligned}\]

El recíproco de un número se utiliza para dividir fracciones. Para esto, simplemente se debe hallar el recíproco de la fracción que representa al divisor y, en lugar de efectuar una división, se realiza una multiplicación de fracciones. Por ejemplo, la división de fracciones $\frac{2}{3}\div\frac{3}{-4}$ es equivalente a multiplicar la fracción $\frac{2}{3}$ por el recíproco de $\frac{3}{-4}$, es decir:

\[\begin{aligned}\frac{2}{3}\div\frac{3}{-4}&=\frac{2}{3}\cdot\left(\frac{3}{-4}\right)^{-1}\\&=\frac{2}{3}\cdot\left(-\frac{4}{3}\right)\\&=-\left(\frac{2}{3}\cdot\frac{4}{3}\right)\\&=-\frac{8}{9}\end{aligned}\]

Ejercicios del recíproco de un número

Ejercicio 1. Calcula el recíproco de 10.

Solución. El recíproco de un número real $x$ se denota como $x^{-1}$ y es igual a $\frac{1}{x}$. Es decir, el recíproco de un número se obtiene al dividir 1 entre dicho número. Por lo tanto, el recíproco de 10 es simplemente la fracción $\frac{1}{10}$.

Ejercicio 2. Hallar el recíproco de -9.

Solución: El recíproco de -9 se denota como $(-9)^{-1}$ y es igual a $-\frac{1}{9}$. Este resultado se obtiene al dividir 1 entre -9 y aplicar la ley de los signos para la división, es decir: \[\begin{aligned}(-9)^{-1}&=\frac{1}{-9}\\&=\frac{+1}{-9}\\&=-\frac{1}{9}\end{aligned}\]

Ejercicio 3. Calcular el recíproco de $-\frac{1}{2}$.

Solución: Observa que se trata de una fracción negativa con numerador 1. El recíproco se obtiene al dividir 1 entre la fracción $-\frac{1}{2}$, es decir: \[\begin{aligned}\left(-\frac{1}{2}\right)^{-1}&=\frac{1}{-\frac{1}{2}}\\&=\frac{\frac{1}{1}}{-\frac{1}{2}}\\&=-\frac{2\cdot 1}{1\cdot 1}\\&=-\frac{2}{1}\\&=-2\end{aligned}\]

Otra forma de obtener el recíproco de la fracción es invertir el numerador y el denominador, de tal manera que: \[-\frac{1}{2}=-\frac{2}{1}\]

Ejercicio 4. Hallar el recíproco del número negativo -3.

Solución: El recíproco del número negativo -3 se denota como $(-3)^{-1}$ y se obtiene al dividir 1 entre -3 considerando la ley de los signos para la división, es decir: \[\begin{aligned}(-3)^{-1}&=\frac{1}{-3}\\&=\frac{+1}{-3}\\&=-\frac{1}{3}\end{aligned}\] Por lo tanto, el recíproco del número negativo -3 es la fracción $-\frac{1}{3}$.

Ejercicio 5. ¿Cuál es el recíproco de la fracción $\frac{9}{4}$?

Solución: El recíproco de una fracción se obtiene al dividir 1 entre la fracción o, más fácilmente, al invertir la fracción, es decir, pasando el numerador al denominador y el denominador al numerador. Entonces, el recíproco de la fracción $\frac{9}{4}$ es la fracción $\frac{4}{9}$.

Preguntas frecuentes

¿Qué es el recíproco de un número? El recíproco o inverso multiplicativo de un número real $x$ es aquel número que, al multiplicarse por $x$, da como resultado la unidad.

¿Cuál es el recíproco de cero? En el campo de los números reales, el cero no tiene recíproco, ya que no existe ningún número que, al multiplicarse por cero, dé como resultado 1.

¿Cuál es el recíproco de un número fraccionario? El recíproco de un número fraccionario es simplemente la fracción invertida, es decir, se intercambia el numerador y el denominador. Por ejemplo, el recíproco de $\frac{3}{4}$ es $\frac{4}{3}$.

¿Cómo se calcula el recíproco de un número negativo? El recíproco de un número negativo se calcula de la misma manera que el recíproco de un número positivo, es decir, se calcula dividiendo 1 entre el número negativo. Como el divisor es negativo entonces el resultado es una fracción negativa. Por ejemplo, el recíproco de -3 es igual a $-\frac{1}{3}$.

¿Cuál es la relación entre un número y su recíproco en términos de multiplicación? La relación entre un número y su recíproco es que, cuando se multiplican, el resultado siempre es 1. Es decir, para cualquier número real $x$, excepto cuando $x$ es igual a cero, se cumple que: \[\begin{aligned}x\cdot x^{-1}&=\frac{x}{x}\\&=1\end{aligned}\]

¿Cuál es la diferencia entre el recíproco y el inverso de un número? En matemáticas, los términos "recíproco" e "inverso" se utilizan indistintamente y se refieren al mismo concepto: el número que, multiplicado por el original, produce 1.